题目内容
4.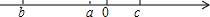 已知a,b,c在数轴上的位置如图:化简代数式$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{({c-a)}^{2}}$+|b+c|的值为( )
已知a,b,c在数轴上的位置如图:化简代数式$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{({c-a)}^{2}}$+|b+c|的值为( )| A. | a | B. | -a | C. | -3a-2b | D. | -3a |
分析 先由数轴上a,b两点的位置,判断出a,b的符号及绝对值的大小,再分别代入各式计算即可.
解答 解:由数轴可得:b<a<0<c,
∴a+b<0,c-a>0,b+c<0,
$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{({c-a)}^{2}}$+|b+c|
=|a|-|a+b|+|c-a|+|b+c|
=-a+a+b+c-a-b-c
=-a.
故选:B.
点评 此题考查了二次根式的化简与性质、绝对值的性质以及实数与数轴的关系.此题难度适中,注意确定a,b之间的大小关系是解此题的关键.

练习册系列答案
相关题目
15.下列各组图形中,一定相似的是( )
| A. | 任意两个矩形 | B. | 任意两个菱形 | ||
| C. | 任意两个直角三角形 | D. | 任意两个等边三角形 |
12.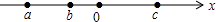 有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
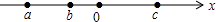 有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )
有理数a、b、c在数轴上对应的点中图所示,则下列式子中正确的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a<-b<c | D. | -a-c>-b-c |
14.计算${({-2})^2}+|{-3}|×\frac{1}{3}$的结果为( )
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
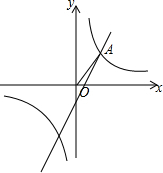 如图,已知反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过M(a,b),N(a+1,b+k)两点.
如图,已知反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过M(a,b),N(a+1,b+k)两点.