题目内容
12. 如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE.
如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE.
分析 先求出∠BAD=∠CAE,再利用“边角边”证明△ABD和△AEC全等,根据全等三角形对应边相等证明即可.
解答 证明:∵∠DAE=∠BAC,
∴∠DAE-∠BAE=∠BAC-∠BAE,
即∠BAD=∠CAE,
在△ABD和△AEC中,$\left\{\begin{array}{l}{AB=AE}\\{∠BAD=∠CAE}\\{AD=AC}\end{array}\right.$,
∴△ABD≌△AEC(SAS),
∴BD=CE.
点评 本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法并求出∠BAD=∠CAE是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,正方形ABCD的边长为10,在正方形ABCD内有一点E,满足∠AEB=90°,AE=6,求阴影部分的面积.
如图,正方形ABCD的边长为10,在正方形ABCD内有一点E,满足∠AEB=90°,AE=6,求阴影部分的面积.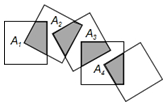 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为$\frac{n-1}{4}$cm2.
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为$\frac{n-1}{4}$cm2. 如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,求证:点O在∠BAC的平分线上.
如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,求证:点O在∠BAC的平分线上.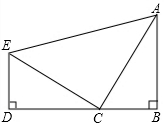 如图,已知△ABC≌△CDE,∠B=∠D=90°,且B,C,D三点在同一条直线.
如图,已知△ABC≌△CDE,∠B=∠D=90°,且B,C,D三点在同一条直线.