题目内容
4.在△ABC中,AB=AC=5,S△ABC=10,求BC.分析 根据题意画出图形,首先利用三角形面积求法得出EC的长,再利用勾股定理得出AE以及BC的长.
解答 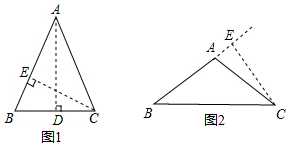 解:如图1,过点A作AD⊥BC于点D,过点C作CE⊥AB于点E,
解:如图1,过点A作AD⊥BC于点D,过点C作CE⊥AB于点E,
∵AB=AC=5,S△ABC=10,
∴$\frac{1}{2}$×EC×AB=10,
解得:EC=4,
∴AE=$\sqrt{A{C}^{2}-E{C}^{2}}$=3,
∴BE=2,
∴BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$;
如图2,过点C作CE⊥AB于点E,
∵AB=AC=5,S△ABC=10,
∴$\frac{1}{2}$×EC×AB=10,
解得:EC=4,
∴AE=$\sqrt{A{C}^{2}-E{C}^{2}}$=3,
∴BE=3+5=8,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=2$\sqrt{10}$.
综上所述,BC的长是2$\sqrt{5}$或2$\sqrt{10}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
19.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表
(1)如表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出x与y之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度.
| 所挂物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧的长度y(cm) | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(2)写出x与y之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度.
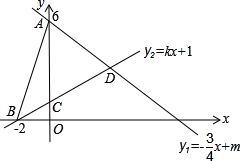 如图,直线l1:y1=-$\frac{3}{4}$x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
如图,直线l1:y1=-$\frac{3}{4}$x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB. 如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE.
如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE. 如图,△ABC中,过点B作射线BF∥AC,已知E点为BC边上一点,D点为射线BF上一点,且AC=BE,BC=BD.
如图,△ABC中,过点B作射线BF∥AC,已知E点为BC边上一点,D点为射线BF上一点,且AC=BE,BC=BD.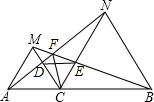 已知,如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,求证:AF=MF+FC.
已知,如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,求证:AF=MF+FC.