题目内容
1.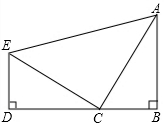 如图,已知△ABC≌△CDE,∠B=∠D=90°,且B,C,D三点在同一条直线.
如图,已知△ABC≌△CDE,∠B=∠D=90°,且B,C,D三点在同一条直线.(1)试说明:BD=AB+ED.
(2)试判定△ACE的形状,并说明理由.
分析 (1)根据全等三角形的性质即可得,BC=DE,AB=CD,根据BD=DC+BC即可得到结论;
(2)根据全等三角形的性质可得∠ACB=∠CED,∠BAC=∠ECD,AC=EC,由∠BAC+∠ACB=90°,推出∠ECD+∠ACB=90°,推出∠ACB=90°,即可得到结论;
解答 证明:(1)∵Rt△ABC≌Rt△CDE,
∴BC=DE,AB=CD,
∵BD=CD+CB,
∴BD=AB+ED.
(2)结论:△ACE是等腰直角三角形.
理由:∵Rt△ABC≌Rt△CDE,∠B=∠D=90°,
∴∠ACB=∠CED,∠BAC=∠ECD,AC=EC,
∵∠BAC+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACB=90°,
∴△ACE是等腰直角三角形.
点评 本题考查了全等三角形的判定和性质、等腰直角三角形的判定,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
6.等腰三角形的腰长13,底边长为24,则底边上的高是( )
| A. | 6 | B. | 7 | C. | 5 | D. | 4 |
10.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE.
如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE. 如图,△ABC中,过点B作射线BF∥AC,已知E点为BC边上一点,D点为射线BF上一点,且AC=BE,BC=BD.
如图,△ABC中,过点B作射线BF∥AC,已知E点为BC边上一点,D点为射线BF上一点,且AC=BE,BC=BD.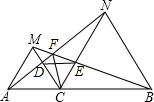 已知,如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,求证:AF=MF+FC.
已知,如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,求证:AF=MF+FC.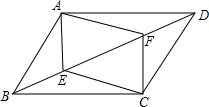 如图,在?ABCD中,已知点E、F在对角线边BD上,且BE=DF,求证:四边形AECF是平行四边形.
如图,在?ABCD中,已知点E、F在对角线边BD上,且BE=DF,求证:四边形AECF是平行四边形.