题目内容
7. 如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,求证:点O在∠BAC的平分线上.
如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,求证:点O在∠BAC的平分线上.
分析 先根据条件可以得出△BOD≌△COE,由全等三角形的性质得到OD=OE,又OD⊥AB,OE⊥AC,利用角平分线的定义可得结论.
解答 证明:∵BE、CD是△ABC的两条高,
∴OD⊥AB,OE⊥AC,∠BDO=∠CEO=90°,
在△BDO和△CEO中$\left\{\begin{array}{l}∠BDO=∠CEO\\∠BOD=∠COE\\ OB=OC\end{array}\right.$
∴△BDO≌△CEO,
∴OD=OE,
又∵OD⊥AB,OE⊥AC,
∴点O在∠BAC的平分线上.
点评 此题主要考查角平分线的定义和全等三角形的判定和性质,证得OD=OE是解答此题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
1.在Rt△ABC中,∠C=90°,若∠A=30°,AB=12cm,则BC边的长为( )
| A. | 6 cm | B. | 12 cm | C. | 24 cm | D. | 无法确定 |
2.下列调查中,最适合采用抽样调查的是( )
| A. | 调查我市居民对汽车废气污染环境的看法 | |
| B. | 对全班同学的身高情况进行调查 | |
| C. | 乘坐高铁对旅客的行李的检查 | |
| D. | 对学校的卫生死角进行调查 |
19.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表
(1)如表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出x与y之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度.
| 所挂物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧的长度y(cm) | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(2)写出x与y之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度.
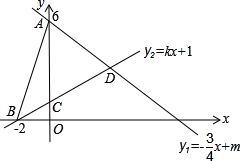 如图,直线l1:y1=-$\frac{3}{4}$x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
如图,直线l1:y1=-$\frac{3}{4}$x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB. 如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE.
如图,在△ABC和△DAE中,∠DAE=∠BAC,AB=AE,AD=AC,连接BD、CE.求证:BD=CE.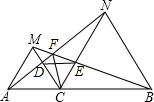 已知,如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,求证:AF=MF+FC.
已知,如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,求证:AF=MF+FC.