题目内容
3．
如图，△ABC是等边三角形，点D在CB的延长线上，且BD=BE，则∠BED=30°．
分析 由等边三角形的性质可知∠ABC=60°，根据BE=BD可得∠BDE=∠BED，由外角性质可得∠BDE+∠BED=∠ABC，即可求得∠BED=30°．
解答 解：∵△ABC是等边三角形，
∴∠ABC=60°，
∵BE=BD，
∴∠BDE=∠BED，
∵∠BDE+∠BED=∠ABC，
∴∠BED=∠BDE=30°．
故答案为：30°．
点评 本题考查了等边三角形的性质和等腰三角形底角相等的性质，得出∠BDE=∠BED是解题的关键．
练习册系列答案
相关题目
13．方程2x2-4x-1=0经过配方化为（x+a）2=b的形式，则正确的是（ ）
| A． | 2（x-1）2=-3 | B． | 2（x-1）2=3 | C． | （x-1）2=-$\frac{3}{2}$ | D． | （x-1）2=$\frac{3}{2}$ |
15．
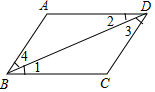如图，下列说法正确的是（ ）
如图，下列说法正确的是（ ）| A． | 若AB∥CD，则∠1=∠2 | B． | 若AD∥BC，则∠3=∠4 | C． | 若∠1=∠2，则AB∥CD | D． | 若∠1=∠2，则AD∥BC |