题目内容
一艘轮船在A处，北偏东45°．方向上有一灯塔P，轮船沿着北偏西30°方向航行4小时达到B处，这时灯塔P正好在轮船的正东方向上，已知轮船的航速为25海里/小时，求轮船在B处时与灯塔P的距离（结果保留根号）
考点：解直角三角形的应用-方向角问题
专题：数形结合
分析：可做AC⊥BP，从而构造两个直角三角形，再根据特殊角的三角函数值解答即可．
解答：
解：作AC⊥BP，在Rt△ABC中，∠BAC=30°，AB=25×4=100，
∴BC=50，AC=50
，
在Rt△ACP中，∠CAP=∠APC=45°，
∴CP=AC=50
．
∴BP=BC+CP=50+50
．
答：轮船在B处时与灯塔P的距离为（50+50
）海里．
解：作AC⊥BP，在Rt△ABC中，∠BAC=30°，AB=25×4=100，∴BC=50，AC=50
| 3 |
在Rt△ACP中，∠CAP=∠APC=45°，
∴CP=AC=50
| 3 |
∴BP=BC+CP=50+50
| 3 |
答：轮船在B处时与灯塔P的距离为（50+50
| 3 |
点评：本题主要考查方向角问题，解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
优加精卷系列答案
相关题目
如图所示的三个图形分别是等边三角形、正方形、长方形，其中AB=CD=EG，请你利用这三个图形拼接出不同立体图形展开图的示意图（至少画出四种，可以只利用其中一种图形拼接；所用图形的个数不限）．
如图中有四个面积相同的圆，每个圆的面积都记为S，∠ABC的两边分别经过圆心O1、O2、O3和O4，四个圆盖的面积为5（S-1），∠ABC内部被圆盖住的面积为8，阴影部分的面积为S1、S2、S3满足关系式：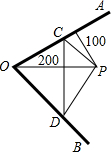
如图，两条河交汇于O点，夹75°角，旅行家住在P点，离O点200m，离河岸AO100cm．他希望到AO上任一点处欣赏风光，再折到河岸BO上任一点D处眺望景物，然后回到住地，则旅行家最少要走在圆中，弦长为2且半径为2围成的弓形的面积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|