题目内容
3. 小明的爸爸新买了一个肩带长度可以调整的单肩包,我们约定单价包自然下垂时肩带的最高点到包的下底边的距离称为包的高度,细心的小明测量发现:
小明的爸爸新买了一个肩带长度可以调整的单肩包,我们约定单价包自然下垂时肩带的最高点到包的下底边的距离称为包的高度,细心的小明测量发现:①肩带调到最长时包的最大高度也与肩带调到最短时包的最小高度之比为5:4;
②爸爸自然站立将肩带调到最长挂到肩上时包的下底边离地69cm;
③爸爸自然站立将肩带调到最短提在手上(手臂自然下垂)时包的下底边离地16cm;
④爸爸提包时臂长为68cm,头顶到肩膀28cm.
求小明爸爸的身高和包的最大高度.
分析 利用小明爸爸的身高=提包时臂长68cm+头顶到肩膀28cm+包的最小高度+包的下底边离地距离得出等式,以及小明爸爸的身高=头顶到肩膀28cm+包的最大高度+包的下底边离地距离得出等式求出即可.
解答 解:设肩带调到最长时包的最大高度为5xcm,小明爸爸的身高为ycm,
则肩带调到最短时包的最小高度为:4xcm,由题意得:
$\left\{\begin{array}{l}{28+68+4x+16=y}\\{5x+28+69=y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=15}\\{y=172}\end{array}\right.$,
即5x=75.
答:肩带调到最长时包的最大高度为75cm,小明爸爸的身高为172cm.
点评 此题主要考查了二元一次方程组的应用,根据题意表示出爸爸的身高进而得出等量关系是解题关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
15.2015年1月20日,参加成都市第十六届人大第三次会议的代表审查了《2015年财政预算草案的报告》,报告显示,2015年教育预算支出为661000万元,数据“661000”用科学记数法表示为( )
| A. | 6.61×105 | B. | 6.61×106 | C. | 66.1×104 | D. | 0.661×106 |
12. 如图,AB∥CD,若∠1=45°,则∠2的度数是( )
如图,AB∥CD,若∠1=45°,则∠2的度数是( )
 如图,AB∥CD,若∠1=45°,则∠2的度数是( )
如图,AB∥CD,若∠1=45°,则∠2的度数是( )| A. | 135° | B. | 90° | C. | 45° | D. | 30° |
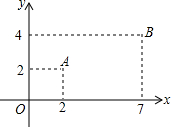 如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴和y轴上行驶.汽车在y轴上行驶到离A村最近的位置的坐标是(0,2);在x轴上行驶到离B村最近时的位置的坐标是(7,0).
如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴和y轴上行驶.汽车在y轴上行驶到离A村最近的位置的坐标是(0,2);在x轴上行驶到离B村最近时的位置的坐标是(7,0).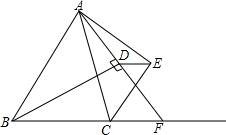 已知:如图,BD为△ABC的内角平分线,CE为△ABC的外角平分线,AD⊥BD于D,AE⊥CE于E,延长AD交BC的延长线于F,连接DE,设BC=a,AC=b,AB=c,(a<b<c)给出以下结论正确的有①③.
已知:如图,BD为△ABC的内角平分线,CE为△ABC的外角平分线,AD⊥BD于D,AE⊥CE于E,延长AD交BC的延长线于F,连接DE,设BC=a,AC=b,AB=c,(a<b<c)给出以下结论正确的有①③.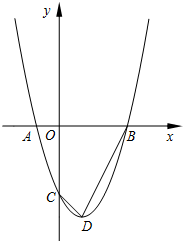 如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.