题目内容
4.若代数式$\frac{3+x}{2}$-1的值不大于$\frac{4x+3}{6}$的值时,求x的取值范围.分析 代数式$\frac{3+x}{2}$-1的值不大于$\frac{4x+3}{6}$的值,则可以列不等式$\frac{3+x}{2}$-1≤$\frac{4x+3}{6}$,解不等式即可求解.
解答 解:根据题意得:$\frac{3+x}{2}$-1≤$\frac{4x+3}{6}$,
去分母,得3(3+x)-6≤4x+3,
去括号,得9+3x-6≤4x+3,
移项,得3x-4x≤3-9+6,
合并同类项,得-x≤0,
系数化成1得x≥0.
点评 本题考查了不等式的解法,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.以上步骤中,只有①去分母和⑤化系数为1可能用到性质3,即可能变不等号方向,其他都不会改变不等号方向.

练习册系列答案
相关题目
12.2tan60°的值是( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
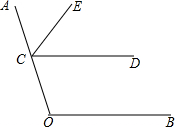 如图,点C在射线OA上,CE平分∠ACD.OF平分∠COB并与射线CD交于点F.
如图,点C在射线OA上,CE平分∠ACD.OF平分∠COB并与射线CD交于点F.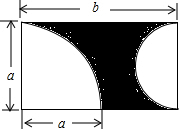 如图,用整式表示图中阴影部分的面积,并计算当a=4cm,b=8cm时的阴影部分的面积(结果保留π)
如图,用整式表示图中阴影部分的面积,并计算当a=4cm,b=8cm时的阴影部分的面积(结果保留π) 如图,在Rt△ABC中,∠C=90°,AB=6cm,AD平分∠BAC,交BC于点D,CD=3cm,则△ABD的面积是多少?
如图,在Rt△ABC中,∠C=90°,AB=6cm,AD平分∠BAC,交BC于点D,CD=3cm,则△ABD的面积是多少?