题目内容
13. 如图,在Rt△ABC中,∠C=90°,AB=6cm,AD平分∠BAC,交BC于点D,CD=3cm,则△ABD的面积是多少?
如图,在Rt△ABC中,∠C=90°,AB=6cm,AD平分∠BAC,交BC于点D,CD=3cm,则△ABD的面积是多少?
分析 过点D作DE⊥AB,由角平分线的性质可知DE=CD=3,再根据S△ABD=$\frac{1}{2}$AB•DE即可得出结论.
解答  解:过点D作DE⊥AB,
解:过点D作DE⊥AB,
∵AD平分∠BAC,
∴DE=CD=3,
S△ABD=$\frac{1}{2}$AB×DE=$\frac{1}{2}$×6×3=9,
所以△ABD的面积为9cm2.
点评 本题考查的是角平分线的性质及三角形的面积公式,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
3.已知:|x|=3,|y|=2,且x>y,则x-y的值为( )
| A. | 5 | B. | 1 | C. | 5或1 | D. | -5或-1 |
1.下列平面图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下列各组线段中,能构成直角三角形的是( )
| A. | 2cm,3cm,4cm | B. | 1cm,1cm,$\sqrt{2}$cm | C. | 5cm,12cm,14cm | D. | $\sqrt{3}$cm,$\sqrt{4}$cm,$\sqrt{5}$cm |
18.已知三角形的3条中位线分别为3cm,4cm,5cm,则这个三角形的面积是( )
| A. | 6cm2 | B. | 10cm2 | C. | 24cm2 | D. | 40cm2 |
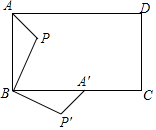 如图,P是矩形ABCD内一点,将△ABP绕点B顺时针方向旋转一定的角度后,AB能与CB重合,如图.若PB=2,AB=3,BC=4,则P P′=2$\sqrt{2}$.
如图,P是矩形ABCD内一点,将△ABP绕点B顺时针方向旋转一定的角度后,AB能与CB重合,如图.若PB=2,AB=3,BC=4,则P P′=2$\sqrt{2}$.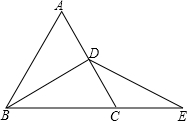 如图,△ABC为等边三角形,BD⊥AC于D,点E在BC的延长线上,且CE=CD,求证:BD=DE.
如图,△ABC为等边三角形,BD⊥AC于D,点E在BC的延长线上,且CE=CD,求证:BD=DE. 画出从正面、上面看到的几何体的形状图.
画出从正面、上面看到的几何体的形状图.