题目内容
 如图,点A是y轴正半轴上的一个定点,点B是反比例函数y=
如图,点A是y轴正半轴上的一个定点,点B是反比例函数y= (x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将
(x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将
- A.逐渐增大
- B.逐渐减小
- C.不变
- D.先增大后减小
A
分析:设B(x,y),则x>0,y>0,△OAB的面积= ×OA×x,由于OA的长度不变,则△OAB的面积随着x的增大而增大.根据反比例函数的增减性可知,函数y=
×OA×x,由于OA的长度不变,则△OAB的面积随着x的增大而增大.根据反比例函数的增减性可知,函数y= 当x>0时,y随x的增大而减小,故当点B的纵坐标y逐渐减小时,点B的横坐标x逐渐增大,进而得出结果.
当x>0时,y随x的增大而减小,故当点B的纵坐标y逐渐减小时,点B的横坐标x逐渐增大,进而得出结果.
解答:根据反比例函数的增减性可知,
反比例函数y= (x>0)图象y随x的增大而减小,
(x>0)图象y随x的增大而减小,
所以OA不变,△OAB的高随着点B的纵坐标逐渐减小而增大,
所以△OAB的面积将逐渐增大.
故选A.
点评:本题主要考查了反比例函数 的增减性:(1)当k>0时,在每一个象限内,y随x的增大而减小;(2)当k<0时,在每一个象限内,y随x的增大而增大.
的增减性:(1)当k>0时,在每一个象限内,y随x的增大而减小;(2)当k<0时,在每一个象限内,y随x的增大而增大.
分析:设B(x,y),则x>0,y>0,△OAB的面积=
 ×OA×x,由于OA的长度不变,则△OAB的面积随着x的增大而增大.根据反比例函数的增减性可知,函数y=
×OA×x,由于OA的长度不变,则△OAB的面积随着x的增大而增大.根据反比例函数的增减性可知,函数y= 当x>0时,y随x的增大而减小,故当点B的纵坐标y逐渐减小时,点B的横坐标x逐渐增大,进而得出结果.
当x>0时,y随x的增大而减小,故当点B的纵坐标y逐渐减小时,点B的横坐标x逐渐增大,进而得出结果.解答:根据反比例函数的增减性可知,
反比例函数y=
 (x>0)图象y随x的增大而减小,
(x>0)图象y随x的增大而减小,所以OA不变,△OAB的高随着点B的纵坐标逐渐减小而增大,
所以△OAB的面积将逐渐增大.
故选A.
点评:本题主要考查了反比例函数
 的增减性:(1)当k>0时,在每一个象限内,y随x的增大而减小;(2)当k<0时,在每一个象限内,y随x的增大而增大.
的增减性:(1)当k>0时,在每一个象限内,y随x的增大而减小;(2)当k<0时,在每一个象限内,y随x的增大而增大. 
练习册系列答案
相关题目
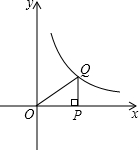 如图,点P是x轴正半轴上的一动点,过点P作x轴的垂线,交双曲线y=
如图,点P是x轴正半轴上的一动点,过点P作x轴的垂线,交双曲线y=| 1 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、保持不变 | D、无法确定 |
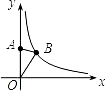 如图,点A是y轴正半轴上的一个定点,点B是反比例函数y=
如图,点A是y轴正半轴上的一个定点,点B是反比例函数y=| 2 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、不变 | D、先增大后减小 |
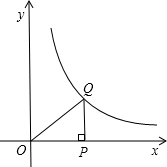 如图,点P是x轴正半轴上一点,过点P作x轴的垂线交函数y=
如图,点P是x轴正半轴上一点,过点P作x轴的垂线交函数y=| 2 |
| x |
| A、逐渐增大 | B、逐渐变小 |
| C、不变 | D、无法判断 |
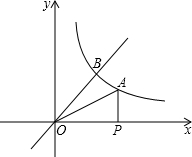 如图,点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线
如图,点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线 (x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( )
(x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( )