题目内容
16.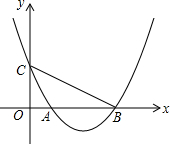 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(4,0)两点,与y轴交于点C(0,2).
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(4,0)两点,与y轴交于点C(0,2).(1)求抛物线的表达式;
(2)求证:∠CAO=∠BCO;
(3)若点P是抛物线上的一点,且∠PCB+∠ACB=∠BCO,求直线CP的表达式.
分析 (1)设抛物线的解析式为为y=a(x-1)(x-4),将点C的坐标代可求得a的值,从而得到抛物线的解析式;
(2)先证明$\frac{OA}{CO}=\frac{OC}{OB}$,从而可证明△AOC∽△COB,由相似三角形的性质可证得∠CAO=∠BCO;
(3)先证明∠PCB=∠CBO,如图2所示可得到CD=BD,然后由勾股定理可求得OD的长,从而得到点D的坐标,由点C和点D的坐标可求得PC的解析式,如图3所示当∠PCB=∠CBO时,PC∥OB,从而可得到PC的解析式.
解答 解:(1)设抛物线的解析式为y=a(x-1)(x-4).
∵将C(0,2)代入得:4a=2,解得a=$\frac{1}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}$(x-1)(x-4),即y=$\frac{1}{2}$x2$-\frac{5}{2}$x+2.
(2)如图1所示:连接AC.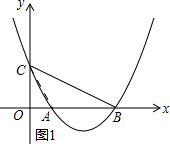
∵由题意可知;OA=1,OC=2,OB=4,
∴$\frac{OA}{OC}=\frac{OC}{OB}=\frac{1}{2}$.
又∵∠COA=∠BOC,
∴△AOC∽△COB.
∴∠CAO=∠BCO.
(3)①如图2所示: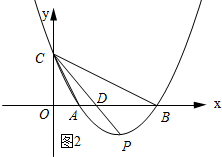
∵∠PCB+∠ACB=∠BCO,∠ACO+∠ACB=∠BCO,
∴∠PCB=∠ACO.
∵△AOC∽△COB,
∴∠ACO=∠CBO.
∴∠PCB=∠CBO.
∴CD=BD.
设OD=x,则DB=CD=4-x.
在Rt△DCO中,由勾股定理得:OD2+CO2=DC2,即x2+22=(4-x)2.解得:x=1.5.
∴点D的坐标为(1.5,0).
设直线CP的解析式为y=kx+b.
∵将(0,2),D(1.5,0)代入得:$\left\{\begin{array}{l}{1.5k+b=0}\\{b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=2}\end{array}\right.$,
∴直线CP的解析式为y=-$\frac{4}{3}$x+2.
如图3所示: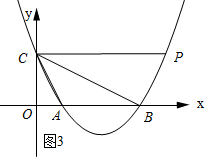
∵∠PCB+∠ACB=∠BCO,∠ACO+∠ACB=∠BCO,
∴∠PCB=∠ACO.
∵△AOC∽△COB,
∴∠ACO=∠CBO.
∴∠PCB=∠CBO.
∴CP∥OB.
∴CP的解析式为y=2.
综上所述,直线CP的解析式为y=-$\frac{4}{3}$x+2或y=2.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数和二次函数的解析式、相似三角形的性质和判定、勾股定理的应用,证得DC=DB,然后依据勾股定理求得OD的长是解题的关键.

| A. | $\frac{40}{7}$ | B. | $\frac{13}{6}$ | C. | $\frac{12}{5}$ | D. | $\frac{22}{7}$ |
| A. | -2x4y4 | B. | 8x4y4 | C. | 16xy4 | D. | 16x4y4 |
| A. | 甲校多于乙校 | B. | 甲校少于乙校 | C. | 甲乙两校一样多 | D. | 不能确定 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | -6 | B. | 6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
 如图,直线a∥b,c∥d,∠1=115°,则∠3=65°.
如图,直线a∥b,c∥d,∠1=115°,则∠3=65°.