题目内容
17.已知a、b、c为有理数,|a|=5,|b|=1,|c-1|=3.(1)直接写出:a=±5;b=±1;c=4或-2.
(2)若ab>0,bc<0,求式子ab-bc-ca的值.
分析 (1)根据“互为相反数的绝对值相等”,即可解答;
(2)根据ab>0,bc<0得到a=5,b=1,c=-2或a=-5,b=-1,c=4,然后把两组分别代入代数式计算即可.
解答 解:(1)∵|a|=5,|b|=1,|c-1|=3.
∴a=±5,b=±1,c=4或-2,
故答案为:±5,±1,4或-2;
(2)∵ab>0,bc<0,a=±5,b=±1,c=4或-2,
∴a=5,b=1,c=-2,或a=-5,b=-1,c=4,
∴ab-bc-ca=5×1-1×(-2)-(-2)×5=5+2+10=17或ab-bc-ca=-5×(-1)-(-1)×4-4×(-5)=5+4+20=29.
点评 本题考查了绝对值,解决本题的关键是熟记绝对值的定义.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
5.下列各组数据中的三个数,可作为三边长构成直角三角形的是( )
| A. | 0.2,0.3,0.4 | B. | 1,1,2 | C. | 6,6,6 | D. | 3,4,5 |
12.将方程-x2-8x=10化为一元二次方程的一般形式,其中二次项系数为1,一次项系数、常数项分别是( )
| A. | -8、-10 | B. | -8、10 | C. | 8、-10 | D. | 8、10 |
9.把(2-x)$\sqrt{\frac{1}{x-2}}$的根号外的(2-x)移入根号内得( )
| A. | $\sqrt{2-x}$ | B. | $\sqrt{x-2}$ | C. | -$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
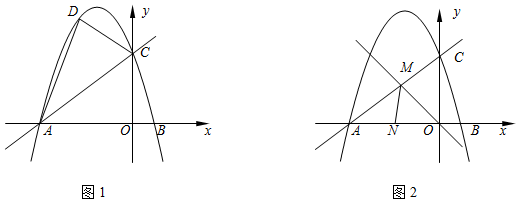
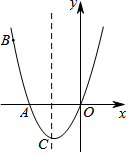 如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线C1经过A(-2,0),B(-3,3)及原点O,顶点为C.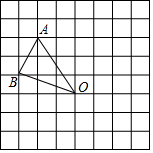 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.