题目内容
如图,四边形AOBC是矩形,点A的坐标是(0,3),点B的坐标是(4,0),动点P,Q同时从点O出发,P沿折线OACB的方向运动,Q沿折线OBCA的方向运动.
(1)若P的运动速度是Q的3倍,点P运动到AC边上,连接PQ交OC于点R,且OR=2,求直线PQ的函数关系式;
(2)若P的运动速度是每秒 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时
个单位长度,运动到相遇时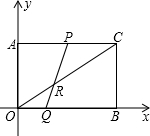 停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
解:(1)设OQ=a,则OA+AP=3a,
OC=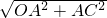 =5,
=5,
∵AC∥OB,
∴△ORQ∽△CRP,
∴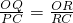 ,
,
∴PC=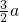 ,
,
∵OA+AC=7,即3a+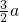 =7,
=7,
∴ ,
,
AP= ,
,
∴P点坐标( ,3),Q点坐标(
,3),Q点坐标(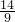 ,0),
,0),
设直线PQ的函数关系式为y=kx+b,
∴ 解得
解得
所以直线PQ的函数关系式是y=27x-42;
(2)当0 时,点P在OA上,点Q在OB上,
时,点P在OA上,点Q在OB上,
S= ×OQ×OP=
×OQ×OP=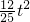 ,
,
当 时,点P在AC上,点Q在OB上,
时,点P在AC上,点Q在OB上,
S= ×
×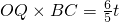 ,
,
当5 时,点P、Q都在BC上,
时,点P、Q都在BC上,
S=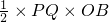 =28-
=28- .
.
分析:(1)设OQ=a,则OA+AP=3a,利用勾股定理易求OC,又AC∥OB,利用平行线分线段成比例定理的推论,可得△ORQ∽△CRP,可得比例线段,从而求出PC=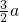 ,从而可知3a+
,从而可知3a+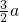 =7,可求a,那么就可得出P、Q的坐标,再利用待定系数法可求出函数解析式;
=7,可求a,那么就可得出P、Q的坐标,再利用待定系数法可求出函数解析式;
(2)分情况讨论,①当0 时,点P在OA上,点Q在OB上,求三角形面积可得函数解析式;②当
时,点P在OA上,点Q在OB上,求三角形面积可得函数解析式;②当 时,点P在AC上,点Q在OB上,求三角形面积可得函数解析式;③当5
时,点P在AC上,点Q在OB上,求三角形面积可得函数解析式;③当5 时,点P、Q都在BC上,求三角形面积可得函数解析式.
时,点P、Q都在BC上,求三角形面积可得函数解析式.
点评:本题考查了勾股定理、平行线分线段成比例定理的推论、相似三角形的判定和性质、待定系数法求函数解析式、三角形的面积公式,难度适中.
OC=
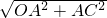 =5,
=5,∵AC∥OB,
∴△ORQ∽△CRP,
∴
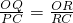 ,
,∴PC=
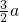 ,
,∵OA+AC=7,即3a+
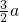 =7,
=7,∴
 ,
,AP=
 ,
,∴P点坐标(
 ,3),Q点坐标(
,3),Q点坐标(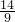 ,0),
,0),设直线PQ的函数关系式为y=kx+b,
∴
 解得
解得
所以直线PQ的函数关系式是y=27x-42;
(2)当0
 时,点P在OA上,点Q在OB上,
时,点P在OA上,点Q在OB上,S=
 ×OQ×OP=
×OQ×OP=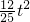 ,
,当
 时,点P在AC上,点Q在OB上,
时,点P在AC上,点Q在OB上,S=
 ×
×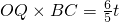 ,
,当5
 时,点P、Q都在BC上,
时,点P、Q都在BC上,S=
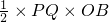 =28-
=28- .
.分析:(1)设OQ=a,则OA+AP=3a,利用勾股定理易求OC,又AC∥OB,利用平行线分线段成比例定理的推论,可得△ORQ∽△CRP,可得比例线段,从而求出PC=
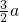 ,从而可知3a+
,从而可知3a+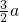 =7,可求a,那么就可得出P、Q的坐标,再利用待定系数法可求出函数解析式;
=7,可求a,那么就可得出P、Q的坐标,再利用待定系数法可求出函数解析式;(2)分情况讨论,①当0
 时,点P在OA上,点Q在OB上,求三角形面积可得函数解析式;②当
时,点P在OA上,点Q在OB上,求三角形面积可得函数解析式;②当 时,点P在AC上,点Q在OB上,求三角形面积可得函数解析式;③当5
时,点P在AC上,点Q在OB上,求三角形面积可得函数解析式;③当5 时,点P、Q都在BC上,求三角形面积可得函数解析式.
时,点P、Q都在BC上,求三角形面积可得函数解析式.点评:本题考查了勾股定理、平行线分线段成比例定理的推论、相似三角形的判定和性质、待定系数法求函数解析式、三角形的面积公式,难度适中.

练习册系列答案
相关题目
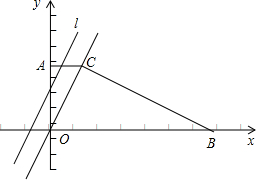 C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.
C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.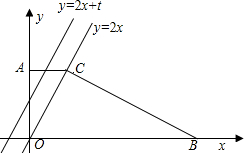 式为y=2x,平行于OC的直线m的解析式为y=2x+t.直线m由A点平移到B点时,m与直角梯形AOBC两边所围成的三角形的面积记为S.
式为y=2x,平行于OC的直线m的解析式为y=2x+t.直线m由A点平移到B点时,m与直角梯形AOBC两边所围成的三角形的面积记为S.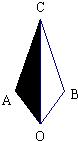 23、如图,四边形AOBC中,∠AOB=72°,∠ACB=36°,OA=OB,AC=BC.以O中心,按顺时针方向,将四边形AOBC旋转72°,请画出依次旋转四次的图形(含阴影部分)
23、如图,四边形AOBC中,∠AOB=72°,∠ACB=36°,OA=OB,AC=BC.以O中心,按顺时针方向,将四边形AOBC旋转72°,请画出依次旋转四次的图形(含阴影部分) 移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R.
移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R. 如图,四边形AOBC中,AC=BC,∠A+∠OBC=180°,CD⊥OA于D.
如图,四边形AOBC中,AC=BC,∠A+∠OBC=180°,CD⊥OA于D.