题目内容
如图,四边形AOBC为直角梯形,OC=| 5 |
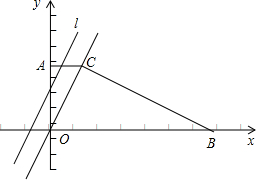 C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.
C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.(1)求点C的坐标;
(2)求t的取值范围;
(3)求出S与t之间的函数关系式.
分析:(1)因为OC=
,OB=5AC,OC所在的直线方程为y=2x,所以可设点C坐标为(x,y),根据勾股定理可得x2+y2=5,再把y=2x代入,即可求出x的值,进而求出答案;
(2)因为平行于OC的直线l为:y=2x+t,l由A点平移到B点,由(1)求出OB的长,即求出了B的坐标,然后分别求出直线过点A(0,2),点B(5,0)时的值,就求出了t的最大值和最小值,从而求出t的范围;
(3)根据直线和OC的位置关系,需个情况讨论:
①当0≤t≤2时,求出l与y轴交于F(0,t),连接OC,利用l∥OC,得到相似三角形,即可找出面积间的关系S:(2×1÷2)=(2-t)2:22,求出答案;
②当-10≤t≤0时,求出l与x轴交于E(-
,0),利用l∥OC,得到相似三角形,即可找出面积间的关系
=(
)2,求出答案.
| 5 |
(2)因为平行于OC的直线l为:y=2x+t,l由A点平移到B点,由(1)求出OB的长,即求出了B的坐标,然后分别求出直线过点A(0,2),点B(5,0)时的值,就求出了t的最大值和最小值,从而求出t的范围;
(3)根据直线和OC的位置关系,需个情况讨论:
①当0≤t≤2时,求出l与y轴交于F(0,t),连接OC,利用l∥OC,得到相似三角形,即可找出面积间的关系S:(2×1÷2)=(2-t)2:22,求出答案;
②当-10≤t≤0时,求出l与x轴交于E(-
| t |
| 2 |
| S | ||
|
5+
| ||
| 5 |
解答:解:(1)设点C坐标为(x,y),根据题意,得:
x2+y2=5,
又因OC所在的直线方程为y=2x,
∴(2x)2+x2=5,
∴x1=1,x2=-1(舍去),
∴C(1,2);
(2)∵C(1,2),
∴OA=2,AC=1,OB=5AC=5,
∴B(5,0),
若y=2x+t过点A(0,2),则t=2,
若y=2x+t过点B(5,0),则t=-10,
∴-10≤t≤2;
(3)有两种情况:
①当0≤t≤2时,
l与y轴交于F(0,t),连接OC,
∵l∥OC,OF=t,AF=2-t,
∴S:(2×1÷2)=(2-t)2:22,
∴S=
(2-t)2
②当-10≤t≤0时,
∵l与x轴交于E(-
,0),
∴OE=-
,BE=5+
,
∵l∥OC
∴
=(
)2,
∴S=
(5+
t)2.
x2+y2=5,
又因OC所在的直线方程为y=2x,
∴(2x)2+x2=5,
∴x1=1,x2=-1(舍去),
∴C(1,2);
(2)∵C(1,2),
∴OA=2,AC=1,OB=5AC=5,
∴B(5,0),
若y=2x+t过点A(0,2),则t=2,
若y=2x+t过点B(5,0),则t=-10,
∴-10≤t≤2;
(3)有两种情况:
①当0≤t≤2时,
l与y轴交于F(0,t),连接OC,
∵l∥OC,OF=t,AF=2-t,
∴S:(2×1÷2)=(2-t)2:22,
∴S=
| 1 |
| 4 |
②当-10≤t≤0时,
∵l与x轴交于E(-
| t |
| 2 |
∴OE=-
| t |
| 2 |
| t |
| 2 |
∵l∥OC
∴
| S | ||
|
5+
| ||
| 5 |
∴S=
| 1 |
| 5 |
| 1 |
| 2 |
点评:本题需仔细分析题意,结合图象,利用平行线间的关系、勾股定理、分情况讨论即可解决问题.

练习册系列答案
相关题目
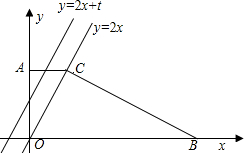 式为y=2x,平行于OC的直线m的解析式为y=2x+t.直线m由A点平移到B点时,m与直角梯形AOBC两边所围成的三角形的面积记为S.
式为y=2x,平行于OC的直线m的解析式为y=2x+t.直线m由A点平移到B点时,m与直角梯形AOBC两边所围成的三角形的面积记为S.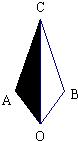 23、如图,四边形AOBC中,∠AOB=72°,∠ACB=36°,OA=OB,AC=BC.以O中心,按顺时针方向,将四边形AOBC旋转72°,请画出依次旋转四次的图形(含阴影部分)
23、如图,四边形AOBC中,∠AOB=72°,∠ACB=36°,OA=OB,AC=BC.以O中心,按顺时针方向,将四边形AOBC旋转72°,请画出依次旋转四次的图形(含阴影部分) 移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R.
移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R. 如图,四边形AOBC中,AC=BC,∠A+∠OBC=180°,CD⊥OA于D.
如图,四边形AOBC中,AC=BC,∠A+∠OBC=180°,CD⊥OA于D.