题目内容
 如图,四边形AOBC中,AC=BC,∠A+∠OBC=180°,CD⊥OA于D.
如图,四边形AOBC中,AC=BC,∠A+∠OBC=180°,CD⊥OA于D.(1)求证:OC平分∠AOB;
(2)若OD=3DA=6,求OB的长.
分析:(1)作CE⊥OB于E,证△ACD≌△BCE,得到CD=CE,即可证得;
(2)证明△OCD≌△OCE,得到OE=OD,根据△ACD≌△BCE,证得BE=AD,即可求解.
(2)证明△OCD≌△OCE,得到OE=OD,根据△ACD≌△BCE,证得BE=AD,即可求解.
解答: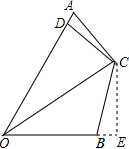 证:(1)作CE⊥OB于E,
证:(1)作CE⊥OB于E,
∵∠A+∠OBC=180°,∠OBC+∠CBE=180°
∴∠A=∠CBE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(AAS),
∴CD=CE,
∴OC平分∠AOB.
(2)∵OD=3DA=6,
∴AD=BE=2,
在Rt△ODC和Rt△OEC中
∵
∴Rt△ODC≌Rt△OEC(HL),
∴OE=OD=6,
∴OB=OE-BE=4.
 证:(1)作CE⊥OB于E,
证:(1)作CE⊥OB于E,∵∠A+∠OBC=180°,∠OBC+∠CBE=180°
∴∠A=∠CBE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(AAS),
∴CD=CE,
∴OC平分∠AOB.
(2)∵OD=3DA=6,
∴AD=BE=2,
在Rt△ODC和Rt△OEC中
∵
|
∴Rt△ODC≌Rt△OEC(HL),
∴OE=OD=6,
∴OB=OE-BE=4.
点评:本题考查了三角形的全等的判定与性质,正确作出辅助线是关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
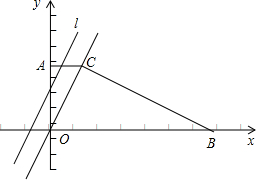 C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.
C的直线l为:y=2x+t,l由A点平移到B点时,l与直角梯形AOBC两边所围成的三角形的面积记为S.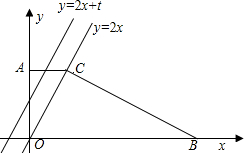 式为y=2x,平行于OC的直线m的解析式为y=2x+t.直线m由A点平移到B点时,m与直角梯形AOBC两边所围成的三角形的面积记为S.
式为y=2x,平行于OC的直线m的解析式为y=2x+t.直线m由A点平移到B点时,m与直角梯形AOBC两边所围成的三角形的面积记为S. 23、如图,四边形AOBC中,∠AOB=72°,∠ACB=36°,OA=OB,AC=BC.以O中心,按顺时针方向,将四边形AOBC旋转72°,请画出依次旋转四次的图形(含阴影部分)
23、如图,四边形AOBC中,∠AOB=72°,∠ACB=36°,OA=OB,AC=BC.以O中心,按顺时针方向,将四边形AOBC旋转72°,请画出依次旋转四次的图形(含阴影部分) 移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R.
移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R.