题目内容
11.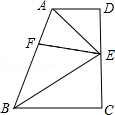 如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分
如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC,过点E作EF⊥AB于F.
(1)求证:△ADE≌△AFE;
(2)求证:DE=EC;
(3)当AD=2,BC=3时,求AB的长.
分析 (1)求出∠AFE=∠D=90°,∠DAE=∠EAF,根据AAS推出即可;
(2)根据AAS推出△BFE≌△BCE,根据全等三角形的性质求出CE=EF,DE=EF,即可得出答案;
(3)延长AE,交BC延长线于M,根据平行线性质求出∠D=∠ECM,根据ASA推出△ADE≌△MCE,求出AD=CM=2,求出AB=BM即可.
解答 (1)证明:∵EF⊥AB,∠D=90°,
∴∠AFE=∠D=90°,
又∵AE平分∠BAD,
∴∠DAE=∠EAF,
在△ADE与△AFE中,
$\left\{\begin{array}{l}{∠D=∠AFE}\\{∠DAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AFE(AAS);
(2)证明:∵BE 平分∠ABC,
∴∠ABE=∠EBC,
∵EF⊥AB,∠C=90°,
∴∠BFE=∠C=90°,
在△BFE与△BCE中,
$\left\{\begin{array}{l}{∠BFE=∠BCE}\\{∠FBE=∠CBE}\\{BE=BE}\end{array}\right.$,
∴△BFE≌△BCE(AAS),
∴EF=EC
又∵△ADE≌△AFE,
∴EF=DE,
∴DE=EC;
(3)解:延长AE,交BC延长线于M,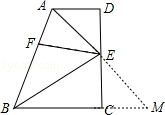
∵AD∥BC,
∴∠D=∠ECM,
在△ADE和△MCE中
$\left\{\begin{array}{l}{∠D=∠ECM}\\{DE=CE}\\{∠AED=∠CEM}\end{array}\right.$
∴△ADE≌△MCE(ASA),
∴AD=CM=2,
∴BM=BC+CM=3+2=5,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∵AD∥BC,
∴∠DAE=∠M,
∴∠EAB=∠M,
∴AB=BM=5.
点评 本题考查了全等三角形的性质和判定平行线的性质,等腰三角形的判定的应用,能根据全等三角形的性质求出DE=EC是解此题的关键,题目比较好,难度适中

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | 野猪 | B. | 蜜蜂 | C. | 松鼠 | D. | 猫 |