题目内容
14.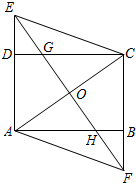 如图,已知在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,交边DC于点G,交边AB于点H.联结AF,CE.
如图,已知在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,交边DC于点G,交边AB于点H.联结AF,CE.(1)求证:四边形AFCE是菱形;
(2)如果OF=2GO,求证:GO2=DG•GC.
分析 (1)根据矩形的性质得到AD∥BC,由平行线的性质得到∠EAC=∠ACF,推出△EOA≌△FOC,根据全等三角形的性质得到AE=CF,OE=OF,推出四边形AFCE是平行四边形,根据菱形的判定定理即可得到结论;
(2)根据相似三角形的性质得到$\frac{EG}{DG}=\frac{CG}{GO}$,等量代换求得结论;
解答 证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAC=∠ACF,
在△EOA和△FOC中,
$\left\{\begin{array}{l}{∠EAC=∠ACF}\\{OA=OF}\\{∠AOE=∠COF}\end{array}\right.$,
∴△EOA≌△FOC,
∴AE=CF,OE=OF,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠EDG=∠COG=90°,∠EGD=∠CGO,
∴△EGD∽△CGO,
∴$\frac{EG}{DG}=\frac{CG}{GO}$,
∵OF=2GO,
∴EG=GO,
∴GO2=DG•GC.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,菱形的判定,矩形的性质,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.为了了解某区5500名初三学生的体重情况,随机抽测了400名学生的体重,统计结果列表如下:
那么样本中体重在50-55范围内的频率是0.21.
| 体重(千克) | 频数 | 频率 |
| 40-45 | 44 | |
| 45-50 | 66 | |
| 50-55 | 84 | |
| 55-60 | 86 | |
| 60-65 | 72 | |
| 65-70 | 48 |
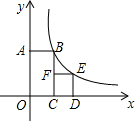 如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )
如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )