题目内容
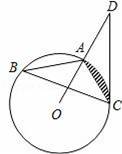
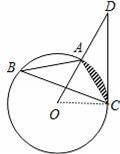
如图,已知△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°,AC=4.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)求阴影部分的面积.

【考点】切线的判定;扇形面积的计算.
【专题】计算题.
【分析】(1)连结OC,如图,根据圆周角定理得到∠AOC=2∠B=60°,则利用三角形内角和可计算出∠OCD=90°,所以OC⊥CD,然后根据切线的判定定理可判断CD为⊙O的切线;
(2)先判断△AOC为等边三角形,则OA=AC=4,然后根据扇形面积公式和等边三角形的面积公式,利用S阴影部分=S扇形AOC﹣S△OAC进行计算.
【解答】解:(1)直线CD为⊙O的切线.理由如下:
连结OC,如图,
则∠AOC=2∠B=60°,
∵∠D=30°,
∴∠OCD=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵OA=OC,∠AOC=60°,
∴△AOC为等边三角形,
∴OA=AC=4,
∴S阴影部分=S扇形AOC﹣S△OAC
=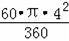
 ﹣
﹣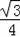
 •42
•42
=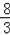
 π﹣4
π﹣4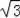
 .
.

【点评】本题考查了切线的判定:切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形面积公式.

练习册系列答案
相关题目

 <
< ,则化简二次根式
,则化简二次根式 的正确结果是( )
的正确结果是( ) B.
B.  C.
C.  D.
D.