��Ŀ����
��ͼ��AD�ǡ�O��ֱ����
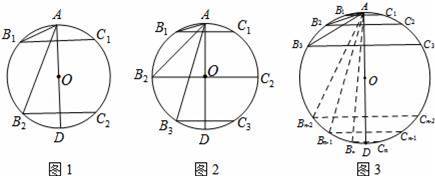
��1����ͼ1����ֱ��AD��������B1C1��B2C2��Բ��4�ȷ֣����B1�Ķ���������������������B2�Ķ�������������������
��2����ͼ2����ֱ��AD��������B1C1��B2C2��B3C3��Բ��6�ȷ֣����B3�Ķ�������������������
��3����ͼ3����ֱ��AD��n����B1C1��B2C2��B3 C3������BnCn��Բ��2n�ȷ֣����Bn�Ķ��������������������ú�n�Ĵ���ʽ��ʾ��Bn�Ķ�������

��
��
�����㡿Բ���ۺ��⣮
����������1�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
��2�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
��3�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
����𡿽⣺��1���ߴ�ֱ��AD��������B1C1��B2C2��Բ��4�ȷ֣�
�B1C1����C1C2����B2C2����B1B2�Ķ�������90�㣬��AB1=��AC1��
�AC1�Ķ�����45�㣬
���B1=
 ��45��=22.5�㣬
��45��=22.5�㣬
��B2=
 ����45��+90�㣩=67.5�㣬
����45��+90�㣩=67.5�㣬
�ʴ�Ϊ��22.5�㣬67.5�㣻
��2���ߴ�ֱ��AD��������B1C1��B2C2��B3C3��Բ��6�ȷ�
�B1C1����C1C2����C2C3�Ķ�������60�㣬��AB1=��AC1��
�AC1�Ķ�����30�㣬
���B3=
 ����30��+60��+60�㣩=75�㣬
����30��+60��+60�㣩=75�㣬
�ʴ�Ϊ��75�㣻
��3���ߴ�ֱ��AD��n����B1C1��B2C2��B3 C3������BnCn��Բ��2n�ȷ֣�
�B1C1����C1C2����C2C3�����Ķ������ǣ�
 ����=��
����=��
 ���㣬��AB1=��AC1��
���㣬��AB1=��AC1��
�AC1�Ķ����ǣ�
 ���㣬
���㣬
���Bn=
 ����
����
 +
+
 +
+
 +��+
+��+
 ��=
��=
 ��[
��[
 +
+
 ]��=90�㩁
]��=90�㩁

�ʴ�Ϊ��90�㩁
 ��
��
�����������⿼����Բ�ܽǶ�����Ӧ�ã�����ȷ���ö������м����ǽ����Ĺؼ���ע�⣺Բ�ĽǵĶ������������ԵĻ��Ķ�����Բ�ܽǵ��������л����Ե�Բ�Ľǵ�һ�룬�Ѷ����У�
��

 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д�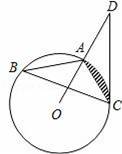




 D��AC2=AD•AB
D��AC2=AD•AB

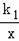
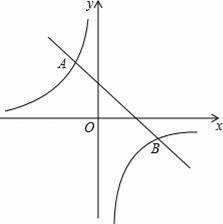
 ��һ�κ���y=k2x+b��ͼ����A��2����1����B��
��һ�κ���y=k2x+b��ͼ����A��2����1����B��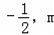
 ����
����

 ��ֵ�� �� ��
��ֵ�� �� �� B��
B�� C��
C�� D��
D��
 ȥ��ĸ
ȥ��ĸ ��ȷ
��ȷ