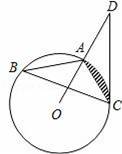
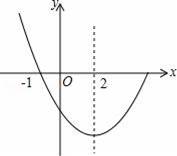
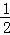题目内容
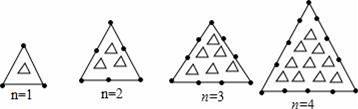
观察下列图形规律:当n= 时,图形“●”的个数和“△”的个数相等.

5
【考点】规律型:图形的变化类.
【专题】规律型.
【分析】首先根据n=1、2、3、4时,“●”的个数分别是3、6、9、12,判断出第n个图形中“●”的个数是3n;然后根据n=1、2、3、4,“△”的个数分别是1、3、6、10,判断出第n个“△”的个数是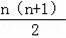
 ;最后根据图形“●”的个数和“△”的个数相等,求出n的值是多少即可.
;最后根据图形“●”的个数和“△”的个数相等,求出n的值是多少即可.
【解答】解:∵n=1时,“●”的个数是3=3×1;
n=2时,“●”的个数是6=3×2;
n=3时,“●”的个数是9=3×3;
n=4时,“●”的个数是12=3×4;
∴第n个图形中“●”的个数是3n;
又∵n=1时,“△”的个数是1=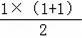
 ;
;
n=2时,“△”的个数是3=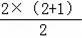
 ;
;
n=3时,“△”的个数是6=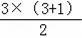
 ;
;
n=4时,“△”的个数是10=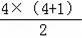
 ;
;
∴第n个“△”的个数是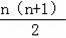
 ;
;
由3n=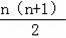
 ,
,
可得n2﹣5n=0,
解得n=5或n=0(舍去),
∴当n=5时,图形“●”的个数和“△”的个数相等.
故答案为:5.
【点评】此题主要考查了规律型:图形的变化类问题,要熟练掌握,解答此类问题的关键是:首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目

 (B)
(B)
 (D)
(D)
 ;②
;② ;③
;③ ;④
;④