题目内容
如图，AB为半圆O的直径，C为半圆上一点，且弧AC为半圆的
，设扇形AOC，△COB，弓形BmC的面积分别为S1，S2，S3，则下列结论正确的是（ ）
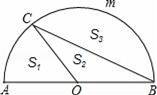
A．S1＜S2＜S3 B．S2＜S1＜S3 C．S2＜S3＜S1 D．S1＜S2＜S3
B【考点】扇形面积的计算．
【分析】首先根据△AOC的面积=△BOC的面积，得S2＜S1．再根据题意，知S1占半圆面积的
．所以S3大于半圆面积的．
【解答】解：根据△AOC的面积=△BOC的面积，得S2＜S1，
再根据题意，知S1占半圆面积的，
所以S3大于半圆面积的．
因此S2＜S1＜S3．
故选：B．
【点评】本题考查了扇形面积的计算．此类题首先要比较有明显关系的两个图形的面积．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
；
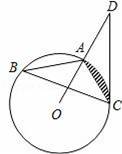
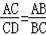
D．AC2=AD•AB