题目内容
 如图,AB为⊙O的直径,与弦CD相交于点E,且AC=2,AE=
如图,AB为⊙O的直径,与弦CD相交于点E,且AC=2,AE=| 3 |
 |
| BD |
考点:垂径定理,弧长的计算,解直角三角形
专题:
分析:连接OC,先根据勾股定理的逆定理判断出△ACE是直角三角形,再由sinA=
=
可得出∠A=30°,故∠COE=60°.再根据sin∠COE=
可得出OC的长,根据AE⊥CD可知
=
,由弧长公式即可得出结论.
| CE |
| AC |
| 1 |
| 2 |
| CE |
| OC |
 |
| BC |
 |
| BD |
解答: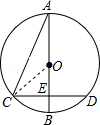 解:连接OC,
解:连接OC,
∵△ACE中,AC=2,AE=
,CE=1,
∴AE2+CE2=AC2,
∴△ACE是直角三角形,即AE⊥CD,
∴sinA=
=
,
∴∠A=30°,
∴∠COE=60°.
∴sin∠COE=
,即
=
,解得OC=
.
∵AE⊥CD,
∴
=
,
∴
的长度l=
=
.
 解:连接OC,
解:连接OC,∵△ACE中,AC=2,AE=
| 3 |
∴AE2+CE2=AC2,
∴△ACE是直角三角形,即AE⊥CD,
∴sinA=
| CE |
| AC |
| 1 |
| 2 |
∴∠A=30°,
∴∠COE=60°.
∴sin∠COE=
| CE |
| OC |
| 1 |
| OC |
| ||
| 2 |
2
| ||
| 3 |
∵AE⊥CD,
∴
 |
| BC |
 |
| BD |
∴
 |
| BD |
60π×
| ||||
| 180 |
2
| ||
| 9 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
以下事件为必然事件的是( )
| A、掷一枚质地均匀的骰子,向上一面的点数是0 |
| B、多边形的内角和是360° |
| C、二次函数的图象必过原点 |
| D、半径为2的圆的周长是4π |
 如图,桌上放着一个圆锥和一个长方体模型,从上面看这两种物品得到的平面图形是( )
如图,桌上放着一个圆锥和一个长方体模型,从上面看这两种物品得到的平面图形是( )



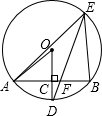 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.