题目内容
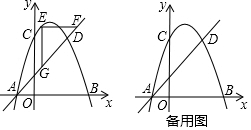
17. 如图,在平面直角坐标系xOy中,抛物线y=x2-(1-m)x+3m经过点A(-1,0),且与y轴相交于点B.
如图,在平面直角坐标系xOy中,抛物线y=x2-(1-m)x+3m经过点A(-1,0),且与y轴相交于点B.(1)求这条抛物线的表达式及点B的坐标;
(2)设点C是所求抛物线上一点,线段BC与x轴正半轴相交于点D,如果$\frac{BD}{CD}$=$\frac{3}{5}$,求点C的坐标;
(3)在(2)条件下,联结AC,求∠ABC的度数.
分析 (1)把A(-1,0)代入y=x2-(1-m)x+3m得到m=-1,于是得到结论;
(2)过C作CE⊥x轴于E,则CE∥y轴,根据相似三角形的性质得到$\frac{OD}{DE}$=$\frac{3}{CE}$=$\frac{3}{5}$,得到CE=5,把y=5代入y=x2-2x-3即可得到结论;
(3)解方程x2-2x-3=0得到x1=-1,x2=3,根据勾股定理得到AC2=(4+1)2+52=50,DE=$\frac{5}{2}$,DC=$\sqrt{(\frac{5}{2})^{2}+{5}^{2}}$=$\frac{5\sqrt{5}}{2}$,BC=$\sqrt{(5+3)^{2}+{4}^{2}}$=4$\sqrt{5}$,根据相似三角形的性质即可得到结论.
解答  解:(1)把A(-1,0)代入y=x2-(1-m)x+3m得:0=(-1)2+(1-m)+3m,
解:(1)把A(-1,0)代入y=x2-(1-m)x+3m得:0=(-1)2+(1-m)+3m,
解得:m=-1,
∴抛物线的表达式y=x2-2x-3,当x=0时,y=-3,
∴B的坐标为(0,-3);
(2)过C作CE⊥x轴于E,则CE∥y轴,
∴△BDO∽△CDE,
∴$\frac{BD}{CD}$=$\frac{BO}{CE}$=$\frac{OD}{DE}$,即$\frac{OD}{DE}$=$\frac{3}{CE}$=$\frac{3}{5}$,
∴CE=5,
把y=5代入y=x2-2x-3得:x1=-2(舍去),x2=4,
∴C(4,5);
(3)解方程x2-2x-3=0得:x1=-1,x2=3,
∴A(-1,0),
∵B(0,-3),C(4,5),
∴AC2=(4+1)2+52=50,
∵$\frac{OD}{DE}$=$\frac{3}{5}$,OD+DE=4,
∴DE=$\frac{5}{2}$,
∴DC=$\sqrt{(\frac{5}{2})^{2}+{5}^{2}}$=$\frac{5\sqrt{5}}{2}$,BC=$\sqrt{(5+3)^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴DC•BC=50,
∴AC2=DC•BC,
∵∠ACD=∠BCA,
∴△CDA∽△CBA,
∴∠ABC=∠CAD,
∵CE=AE=5,
∴∠CAD=45°,
∴∠ABC=45°.
点评 本题考查了相似三角形的判定和性质,勾股定理,待定系数法确定函数关系式,正确的作出辅助线是解题的关键.

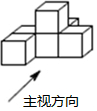 由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )| A. | 左视图与主视图相同 | B. | 俯视图与主视图相同 | ||
| C. | 左视图与俯视图相同 | D. | 三个视图都相同 |
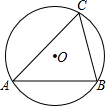 如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )
如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
 已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
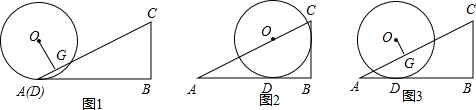
 已知抛物线y=x2-2x-3的大致图象如图所示,与x轴交于A,B两点(A在B左侧),与y轴交于C点,E点在抛物线对称轴上,纵坐标为-3,在该抛物线上有一点D,x轴上有一点F,若以A、E、F、D为顶点的四边形为平行四边形.求符合条件的F点坐标.
已知抛物线y=x2-2x-3的大致图象如图所示,与x轴交于A,B两点(A在B左侧),与y轴交于C点,E点在抛物线对称轴上,纵坐标为-3,在该抛物线上有一点D,x轴上有一点F,若以A、E、F、D为顶点的四边形为平行四边形.求符合条件的F点坐标.