题目内容
2. 已知抛物线y=x2-2x-3的大致图象如图所示,与x轴交于A,B两点(A在B左侧),与y轴交于C点,E点在抛物线对称轴上,纵坐标为-3,在该抛物线上有一点D,x轴上有一点F,若以A、E、F、D为顶点的四边形为平行四边形.求符合条件的F点坐标.
已知抛物线y=x2-2x-3的大致图象如图所示,与x轴交于A,B两点(A在B左侧),与y轴交于C点,E点在抛物线对称轴上,纵坐标为-3,在该抛物线上有一点D,x轴上有一点F,若以A、E、F、D为顶点的四边形为平行四边形.求符合条件的F点坐标.
分析 先求出A、E的坐标,以A、E、F、D为顶点的四边形为平行四边形,只需要按照AE是边或AE是对角线进行讨论即可.
解答 解:令y=0代入y=x2-2x-3,
∴0=x2-2x-3,
解得:x=-1或x=3,
∴A(-1,0)
令x=0代入y=x2-2x-3,
∴y=-3,
∴C(0,-3)
对称轴为x=1,
∴E(1,-3)
当AE是平行四边形的边时,
连接CE,此时CE∥x轴,且交抛物线于点D,
过D作DF∥AE,交x轴于点F,
此时AF=ED=1
当D在对称轴右侧时,
此时F(0,0)
当点D在对称轴左侧时,
此时D与C重合,
∴F(-2,0)
当AE是平行四边形的对角线时,
此时AF=DE=1,
∴F(0,0)
综上所述,F(0,0)或(-2,0).
点评 本题考查平行四边形的综合问题,解题的关键是根据已知的线段AE进行分类讨论,本题属于中等题型.

练习册系列答案
相关题目
6.拒绝“餐桌浪费”刻不容缓,据统计全国每年浪费食物总量约500千万千克,这个数用科学记数法表示为( )
| A. | 0.5×1011千克 | B. | 50×109千克 | C. | 5×109千克 | D. | 5×1010千克 |

 如图,在平面直角坐标系xOy中,抛物线y=x2-(1-m)x+3m经过点A(-1,0),且与y轴相交于点B.
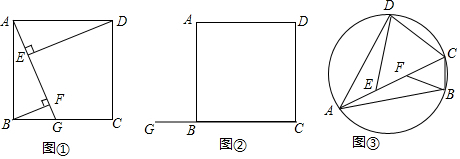
如图,在平面直角坐标系xOy中,抛物线y=x2-(1-m)x+3m经过点A(-1,0),且与y轴相交于点B. 定义:有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
定义:有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F. 我国古代数学中有一道数学题:如图,有一棵枯树直立在地上,树高20尺,粗3尺,有一根藤条从树根处缠绕而上,缠绕5周到达树顶,则这条树藤有25尺.
我国古代数学中有一道数学题:如图,有一棵枯树直立在地上,树高20尺,粗3尺,有一根藤条从树根处缠绕而上,缠绕5周到达树顶,则这条树藤有25尺.