题目内容
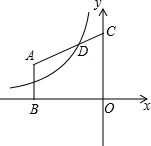 如图,点A在反比例函数y=
如图,点A在反比例函数y=| 3 |
| x |
| A、3 | B、4 | C、6 | D、9 |
考点:反比例函数系数k的几何意义
专题:
分析:设D(m,n),根据反比例函数系数K的几何意义求得mn=-3,作DE⊥x轴,从而求得DE是梯形的中位线,根据中位线的性质求得AB+CO=2DE,OB=2OE,进而根据梯形的面积公式即可求得四边形ABOC的面积.
解答: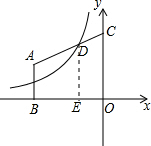 解:设D(m,n),
解:设D(m,n),
∵点D在反比例函数的图象上,
∴mn=-3,
作DE⊥x轴,
∵AB⊥x轴,
∴AB∥DE∥CO,
∴四边形ABOC是梯形,
∵D是AC的中点,
∴DE是梯形的中位线,
∴AB+CO=2DE=2n,OB=2OE=-2m,
∵S=
(AB+CO)•OB,
∴S=
×2DE×2OE=2DE•OE=
×|2n×(-2m)|=6,
故选C.
 解:设D(m,n),
解:设D(m,n),∵点D在反比例函数的图象上,
∴mn=-3,
作DE⊥x轴,
∵AB⊥x轴,
∴AB∥DE∥CO,
∴四边形ABOC是梯形,
∵D是AC的中点,
∴DE是梯形的中位线,
∴AB+CO=2DE=2n,OB=2OE=-2m,
∵S=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查了反比例函数系数K的几何意义,梯形的判定和梯形的中位线的性质,以及梯形的面积等,作出辅助线是本题的关键.

练习册系列答案
相关题目
 如图:已知平行四边形ABCD中,K是BC上一点,且
如图:已知平行四边形ABCD中,K是BC上一点,且| BK |
| KC |
| 3 |
| 4 |
| BE |
| ED |
A、
| ||
B、
| ||
C、
| ||
D、
|
给出下列说法:①0是整数;②-3.2是负分数;③5.6不是正数;④自然数一定是正数;⑤负分数一定是负有理数.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |

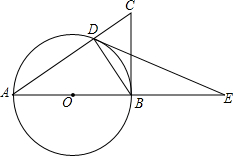 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,交AC于点D,点E是AB延长线上的一点,且∠BDE=∠A.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,交AC于点D,点E是AB延长线上的一点,且∠BDE=∠A.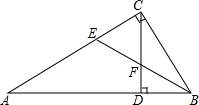 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的
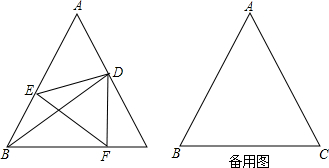
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的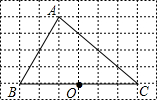 如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.
如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点. 如图,A、D是直线l1上两点,B、C是直线l2上两点,且AB⊥BC,CD⊥AD.
如图,A、D是直线l1上两点,B、C是直线l2上两点,且AB⊥BC,CD⊥AD.