题目内容
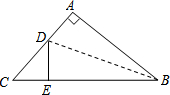 如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则sin∠DBE的值为( )
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则sin∠DBE的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:翻折变换(折叠问题)
专题:
分析:先根据勾股定理求出BC的长,再根据折叠的性质得出△ABD≌△EBD,设AD=DE=x,利用三角形的面积求出AD的长,再利用勾股定理即可求出BD的长,进而可得出结论.
解答:解:∵在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,
∴BC=
=10cm.
∵△EBD由△ABD折叠而成,
∴AD=DE,AB=BE=8cm,∠BED=∠A=90°,
∴设AD=DE=x,则CD=6-x,
∵CE2+DE2=CD2,即(10-8)2+x2=(6-x)2,
解得x=
,即AD=DE=
,
∴BD=
=
=
,
∴sin∠DBE=
=
.
故选:D.
∴BC=
| 62+82 |
∵△EBD由△ABD折叠而成,
∴AD=DE,AB=BE=8cm,∠BED=∠A=90°,
∴设AD=DE=x,则CD=6-x,
∵CE2+DE2=CD2,即(10-8)2+x2=(6-x)2,
解得x=
| 8 |
| 3 |
| 8 |
| 3 |
∴BD=
| DE2+BE2 |
(
|
8
| ||
| 3 |
∴sin∠DBE=
| DE |
| BD |
| ||
| 10 |
故选:D.
点评:此题主要考查了图形的翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.以及勾股定理,锐角三角函数的意义等知识点.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如果代数式-2a+3b+18=8,那么代数式9b-6a+2的值是( )
| A、28 | B、-28 |
| C、32 | D、-32 |
下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是5、12,那么斜边必是13;
③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
②如果直角三角形的两边是5、12,那么斜边必是13;
③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a,b,c(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
| A、①② | B、①③ | C、①④ | D、②④ |
若一次函数y=(1-2k)x-k的函数值y随x的增大而增大,且此函数的图象不经过第二象限,则k的取值范围是( )
A、k<
| ||
| B、k≥0 | ||
C、0≤k<
| ||
D、k≤0或k>
|