题目内容
15．方程$\frac{x-5}{x}$+$\frac{2x+1}{2x}$=0的解是$\frac{9}{4}$．分析 根据解分式方程的步骤，即可解答．
解答 解：在方程两边同乘2x得：2（x-5）+2x+1=0，
解得：x=$\frac{9}{4}$，
检验：当x=$\frac{9}{4}$时，2x≠0，
∴分式方程的解为：x=$\frac{9}{4}$．
故答案为：$\frac{9}{4}$．
点评 本题考查了分式方程的解，解决本题的关键是解分式方程．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
某企业生产并销售某种产品，假设销售量与产量相等，图中的线段AB表示该产品每千克生产成本y1（单位：元）与产量x（单位：kg）之间的函数关系；线段CD表示该产品销售价y2（单位：元）与产量x（单位：kg）之间的函数关系，已知0＜x≤120，m＞60．
6．
如图，在扇形AOB中，∠AOB=90°，半径OA=6，将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，则整个阴影部分的面积为（ ）
如图，在扇形AOB中，∠AOB=90°，半径OA=6，将扇形AOB沿过点B的直线折叠，点O恰好落在弧AB上点D处，折痕交OA于点C，则整个阴影部分的面积为（ ）| A． | 9π-9 | B． | 9π-6$\sqrt{3}$ | C． | 9π-18 | D． | 9π-12$\sqrt{3}$ |
已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A（2，b）、B（-3，m）两点（点A在第一象限），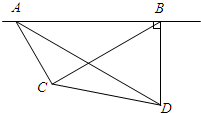
如图，在我市的上空一架飞机由A向B沿水平直线方向飞行，沿航线AB的正下方有两个景点水城明珠大剧院（记为点C），光岳楼（记为点D），飞机在A处时，测得景点C、D在飞机的前方，俯角分别为60°和30°．飞机飞行了3千米到B处时，往后测得景点C的俯角为30°．而景点D恰好在飞机的正下方，求水城明珠大剧院与光岳楼之间的距离（最后结果精确到0.1千米）
7．下列运算结果正确的是（ ）
| A． | （2x3）2=4x6 | B． | x2+x3=x5 | C． | （-x）-1=$\frac{1}{x}$ | D． | x0=1 |
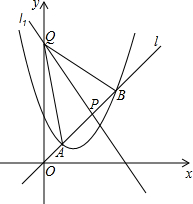已知抛物线C：y=x2-3x+m，直线l：y=kx（k＞0），当k=1时，抛物线C与直线l只有一个公共点．