��Ŀ����
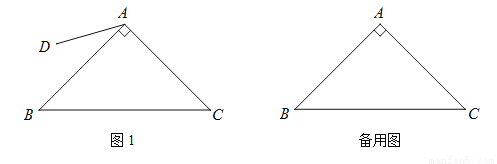
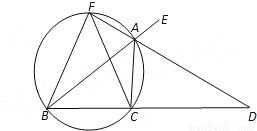
��ͼ����Rt��ABC�У���BAC=90�㣬AB=AC����ƽ������ȡһ��D������AD��AD��AB�������߶�AD�Ƶ�A��ʱ����ת90�㣬�õ��߶�AE������DE��CE��BD��
��1����������ⲹȫͼ1��
��2���²�BD��CE��������ϵ��֤����
��3��������BD��CE���ڵ�P���ѡ�ADE�Ƶ�A��ת������EAC=90�㣬AB=2��AD=1ʱ����ȫͼ�Σ�ֱ��д��PB�ij���
��ϰ��ϵ�д�
�����Ŀ


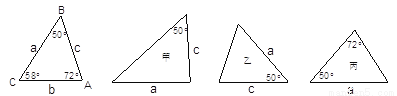
 ������������εĵ�Ϊ___________
������������εĵ�Ϊ___________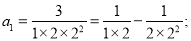
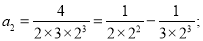
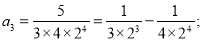
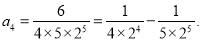
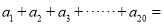 __________________��
__________________��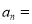 ____________________________��
____________________________�� �����壬��x_________ʱ����ʽ
�����壬��x_________ʱ����ʽ ��ֵ����.
��ֵ����.
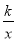 ��k��0��x��0����ͼ����ֱ��y=2x��2���ڵ�Q��2��m����
��k��0��x��0����ͼ����ֱ��y=2x��2���ڵ�Q��2��m����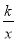 ��ͼ���ڵ�N��
��ͼ���ڵ�N��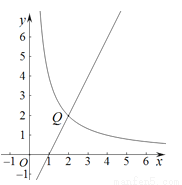
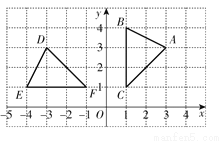
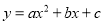 ��ͼ��ȫ����x����·�����ô�����ж�����ȷ����
��ͼ��ȫ����x����·�����ô�����ж�����ȷ����