题目内容
18.由下列条件解直角三角形:在Rt△ABC中,∠C=90°:(1)已知a=4,b=8;
(2)已知b=10,∠B=60.
分析 (1)先利用勾股定理计算出c,然后根据∠A的正切的定义求出∠A的度数,再利用互余计算出∠B的度数;
(2)先利用互余计算出∠A,再利用∠B的正切求出a,然后根据∠A的正弦计算出c.
解答 解:(1)c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∵tanA=$\frac{a}{b}$=$\frac{4}{8}$=0.5,
∴∠A≈27°,
∴∠B=90°-∠A=63°;
(2)∠A=∠C-∠B=90°-60°=30°,
∵tanB=$\frac{b}{a}$,
∴a=$\frac{10}{tan60°}$=$\frac{10}{\sqrt{3}}$=$\frac{10\sqrt{3}}{3}$,
∵sinA=$\frac{a}{c}$,
∴c=$\frac{\frac{10\sqrt{3}}{3}}{sin30°}$=$\frac{20\sqrt{3}}{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解直角三角形要用到的关系:锐角直角的关系:∠A+∠B=90°;三边之间的关系:a2+b2=c2;边角之间的关系:锐角三角函数关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
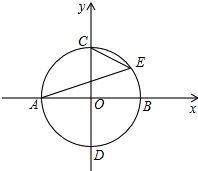 如图,在直角坐标系中,以坐标原点为圆心、半径为2的⊙O与x轴交于A,B两点,与y轴交于C,D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数表达式为y=-x+2,y=x-2..
如图,在直角坐标系中,以坐标原点为圆心、半径为2的⊙O与x轴交于A,B两点,与y轴交于C,D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数表达式为y=-x+2,y=x-2..

 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.
如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.