题目内容
13.抛物线y=ax2-4ax+m与x轴交于(1,0)和(n,0),则n=3.分析 抛物线y=ax2-4ax+m与x轴交于(1,0)和(n,0),则1和n是方程ax2-4ax+m=0的两个根,利用一元二次方程根与系数的关系即可求解.
解答 解:抛物线y=ax2-4ax+m与x轴交于(1,0)和(n,0),
则1和n是方程ax2-4ax+m=0的两个根,
则1+n=-$\frac{-4a}{a}$=4,
解得:n=3.
故答案是:3.
点评 本题考查了二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,二次函数与x轴的两个交点的横坐标就是对应的方程的解.

练习册系列答案
相关题目
18. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC=30°,则∠BAC的度数为( )
如图,AB是⊙O的直径,点C在⊙O上,∠ABC=30°,则∠BAC的度数为( )
 如图,AB是⊙O的直径,点C在⊙O上,∠ABC=30°,则∠BAC的度数为( )
如图,AB是⊙O的直径,点C在⊙O上,∠ABC=30°,则∠BAC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 在图中求一点P,使点到∠AOB两边的距离相等,且到C、D两点的距离也相等,试用直尺、圆规作图,并保留作图痕迹.
在图中求一点P,使点到∠AOB两边的距离相等,且到C、D两点的距离也相等,试用直尺、圆规作图,并保留作图痕迹.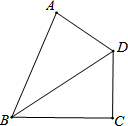 在四边形ABCD中,∠C=90°,∠ABC=∠ADB,BD平分∠ABC,AD:AB=$\sqrt{13}$:6,DC=1,则DB=$\frac{\sqrt{13}}{2}$.
在四边形ABCD中,∠C=90°,∠ABC=∠ADB,BD平分∠ABC,AD:AB=$\sqrt{13}$:6,DC=1,则DB=$\frac{\sqrt{13}}{2}$.