题目内容
3.△ABC内接于⊙O,且AB=AC,点O到BC的距离为3,圆的半径为5,则AB的长是2$\sqrt{5}$或4$\sqrt{5}$.分析 分两种情况考虑:当三角形ABC为锐角三角形时,过A作AD垂直于BC,根据题意得到AD过圆心O,连接OB,在直角三角形OBD中,由OB与OD长,利用勾股定理求出BD的长,在直角三角形ABD中,利用勾股定理即可求出AB的长;当三角形ABC为钝角三角形时,同理求出AB的长,综上即可得到所有满足题意AB的长.
解答 解:分两种情况考虑: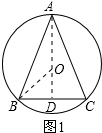
当△ABC为锐角三角形时,如图1所示,
过A作AD⊥BC,由题意得到AD过圆心O,连接OB,
∵OD=3,OB=5,
∴在Rt△OBD中,根据勾股定理得:BD=4,
在Rt△ABD中,AD=AO+OD=8,BD=4,
根据勾股定理得:AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=4$\sqrt{5}$;
当△ABC为钝角三角形时,如图2所示,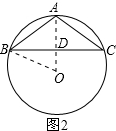
过A作AD⊥BC,由题意得到AD延长线过圆心O,连接OB,
∵OD=3,OB=5,
∴在Rt△OBD中,根据勾股定理得:BD=4,
在Rt△ABD中,AD=AO-OD=2,BD=4,
根据勾股定理得:AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$,
综上,AB=2$\sqrt{5}$或4$\sqrt{5}$.
故答案为:2$\sqrt{5}$或4$\sqrt{5}$.
点评 考查了垂径定理、勾股定理的应用,正确利用分类讨论的思想,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
14.设a为有理数,则|a|+a的结果( )
| A. | 可能是负数 | B. | 不可能是负数 | ||
| C. | 必定是正数 | D. | 可能是正数,也可能是负数 |
18.下列事件中,是必然事件的是( )
| A. | 任意抛掷一枚硬币,出现正面 | |
| B. | 从2、4、6、8、10这5张卡片中任抽一张是奇数 | |
| C. | 从装有一个红球三个黄球的袋子中任取两球,至少有一个是黄球 | |
| D. | 投掷一枚普通骰子,朝上一面的点数是3 |
12.对于抛物线y=-$\frac{1}{3}$(x-5)2+3,下列说法正确的是( )
| A. | 开口向上,对称轴是直线x=5 | B. | 开口向下,对称轴是直线x=-5 | ||
| C. | 开口向上,对称轴是直线x=-5 | D. | 开口向下,对称轴是直线x=5 |
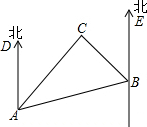 海面上的A,B,C三艘船的平面图如图所示,C船在A船的北偏东55°方向,B船在A船的北偏东85°方向,C船在B船的北偏西25°方向.
海面上的A,B,C三艘船的平面图如图所示,C船在A船的北偏东55°方向,B船在A船的北偏东85°方向,C船在B船的北偏西25°方向.