题目内容
4. 已知:如图,在△ABC中,AD是高,EF是BC的垂直平分线,EF交AC于E,交BC于F,BE交AD于M.求证:点E在AM的垂直平分线上.
已知:如图,在△ABC中,AD是高,EF是BC的垂直平分线,EF交AC于E,交BC于F,BE交AD于M.求证:点E在AM的垂直平分线上.
分析 根据线段垂直平分线的性质得到BE=CE,根据等腰三角形的性质得到∠BEF=∠CEF,推出AD∥EF,根据平行线的性质得到∠CEF=∠CAD,∠AME=∠MEF,等量代换得到∠EAM=∠AME,证得AE=ME,于是得到结论.
解答 证明:∵EF是BC的垂直平分线,
∴BE=CE,
∵EF⊥BC,
∴∠BEF=∠CEF,
∵AD⊥BC,
∴AD∥EF,
∴∠CEF=∠CAD,∠AME=∠MEF,
∴∠EAM=∠AME,
∴AE=ME,
∴点E在AM的垂直平分线上.
点评 本题考查了线段垂直平分线的性质,平行线的性质和判定,等腰三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

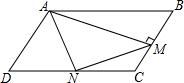 如图,在?ABCD中,N是边DC的中点,AN=3,AM⊥BC交BC于点M,则MN的长是3.
如图,在?ABCD中,N是边DC的中点,AN=3,AM⊥BC交BC于点M,则MN的长是3.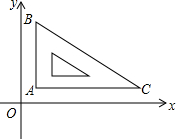 课件、顽皮的小聪把一个直角三角板放在黑板的平面直角坐标系中(如图所示),直角顶点A放在点($\sqrt{3}$,1)处,点A到x轴的距离为1cm,AC∥x轴,AB=6cm,BC=12cm,求BC所在直线的函数表达式.
课件、顽皮的小聪把一个直角三角板放在黑板的平面直角坐标系中(如图所示),直角顶点A放在点($\sqrt{3}$,1)处,点A到x轴的距离为1cm,AC∥x轴,AB=6cm,BC=12cm,求BC所在直线的函数表达式.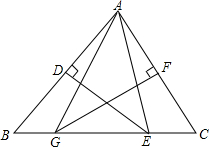 如图,△ABC中,BC=12,∠BAC=70°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G.能否求出∠EAG的度数和△AEG的周长?
如图,△ABC中,BC=12,∠BAC=70°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G.能否求出∠EAG的度数和△AEG的周长?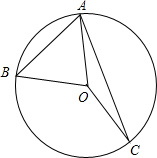 如图,已知点A、B、C在⊙0上,且$\widehat{AB}:\widehat{BC}:\widehat{AC}$=2:3:4.
如图,已知点A、B、C在⊙0上,且$\widehat{AB}:\widehat{BC}:\widehat{AC}$=2:3:4. 如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么?
如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么?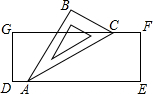 如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.
如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.