题目内容
 如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),直线BC:y=
如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),直线BC:y=| 1 |
| 2 |
(1)⊙A的半径为
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标;
(3)向左移动⊙A(圆心A始终保持在x轴上),与直线BC交于E、F,在移动过程中是否存在点A,使△AEF是直角三角形?若存在,求出点A的坐标;若不存在,请说明理由.
考点:圆的综合题
专题:
分析:(1)如图,连接AC.根据直线BC的解析式易求点B、C的坐标;然后由垂径定理,在直角△AOC中,由勾股定理可以求得半径AC的长度;
(2)过G点作x轴垂线,垂足为H,连接AG,设G(x0,y0),在Rt△ACG中利用锐角三角函数的定义可求出CG的长,
由勾股定理可得出BC的长,由OC∥GH可得出
=
,进而可求出G点坐标;
(3)假设△AEF为直角三角形,由AE=AF可判断出△AEF为等腰三角形,可得出∠EAF=90°,过A作AM⊥BC于M,
在Rt△AEF中利用勾股定理可求出EF的长度,证出△BOC∽△BMA,由相似三角形的性质可得出A点坐标;当圆心A在点B的左侧时,设圆心为A′,过A′作A′M′⊥BC于M′,可得△A′M′B′≌△AMB,由全等三角形的性质可得出A′点的坐标.
(2)过G点作x轴垂线,垂足为H,连接AG,设G(x0,y0),在Rt△ACG中利用锐角三角函数的定义可求出CG的长,
由勾股定理可得出BC的长,由OC∥GH可得出
| OH |
| BO |
| CG |
| BC |
(3)假设△AEF为直角三角形,由AE=AF可判断出△AEF为等腰三角形,可得出∠EAF=90°,过A作AM⊥BC于M,
在Rt△AEF中利用勾股定理可求出EF的长度,证出△BOC∽△BMA,由相似三角形的性质可得出A点坐标;当圆心A在点B的左侧时,设圆心为A′,过A′作A′M′⊥BC于M′,可得△A′M′B′≌△AMB,由全等三角形的性质可得出A′点的坐标.
解答: 解:(1)如图1,连接AC.
解:(1)如图1,连接AC.
∵直线BC的解析式为y=
x+2,
∴当x=0时,y=2.
∴C(0,2).
∴OC=2.
又∵圆心A的坐标为(1,0),
∴OA=1,
∴在直角△AOC中,由勾股定理得到:AC=
=
,即⊙A的半径为
.
故答案是:
;
(2)如图1,过G点作x轴垂线,垂足为H,连接AG,设G(x0,y0),
在Rt△ACG中,∠AGC=60°,AC=
,求得CG=
,
又∵OB=4,
∴BC=
=2
,
∵OC∥GH,
∴
=
,则OH=
,即x0=
,
又∵点G在直线BC上,
∴y0=
×
+2
=
+2,
∴G(
,
+2);
(3)在移动过程中,存在点A,使△AEF为直角三角形.
∵点E、F在⊙A上,
∴AE=AF,
若△AEF为直角三角形,在∠EAF=90°,且为等腰三角形.
过A作AM⊥BC于M,
在Rt△AEF中,EF=
=
,
AM=
EF=
,
证出△BOC∽△BMA得,
=
,
而BC=
=
=2
,OC=2,可得AB=
,
∴OA=4-
,
∴A(-4+
,0),
当圆心A在点B的左侧时,设圆心为A′,
过A′作A′M′⊥BC于M′,可得△A′M′B′≌△AMB,
∴A′B=AB=
,
∴OA′=OB+A′B=4+
,
∴A′(-4-
,0),
∴A(-4+
,0)或A′(-4-
,0).
 解:(1)如图1,连接AC.
解:(1)如图1,连接AC.∵直线BC的解析式为y=
| 1 |
| 2 |
∴当x=0时,y=2.
∴C(0,2).
∴OC=2.
又∵圆心A的坐标为(1,0),
∴OA=1,
∴在直角△AOC中,由勾股定理得到:AC=
| OA2+OC2 |
| 5 |
| 5 |
故答案是:
| 5 |
(2)如图1,过G点作x轴垂线,垂足为H,连接AG,设G(x0,y0),
在Rt△ACG中,∠AGC=60°,AC=
| 5 |
| ||
| 3 |
又∵OB=4,
∴BC=
| OB2+OC2 |
| 5 |
∵OC∥GH,
∴
| OH |
| BO |
| CG |
| BC |
2
| ||
| 3 |
2
| ||
| 3 |

又∵点G在直线BC上,
∴y0=
| 1 |
| 2 |
2
| ||
| 3 |
=
| ||
| 3 |
∴G(
2
| ||
| 3 |
| ||
| 3 |
(3)在移动过程中,存在点A,使△AEF为直角三角形.
∵点E、F在⊙A上,
∴AE=AF,
若△AEF为直角三角形,在∠EAF=90°,且为等腰三角形.
过A作AM⊥BC于M,
在Rt△AEF中,EF=
| AE2+AF2 |
| 10 |
AM=
| 1 |
| 2 |
| ||
| 2 |
证出△BOC∽△BMA得,
| OC |
| AM |
| BC |
| AB |
而BC=
| OC2+OB2 |
| 22+42 |
| 5 |
5
| ||
| 2 |
∴OA=4-
5
| ||
| 2 |
∴A(-4+
5
| ||
| 2 |
当圆心A在点B的左侧时,设圆心为A′,
过A′作A′M′⊥BC于M′,可得△A′M′B′≌△AMB,
∴A′B=AB=
5
| ||
| 2 |
∴OA′=OB+A′B=4+
5
| ||
| 2 |
∴A′(-4-
5
| ||
| 2 |
∴A(-4+
5
| ||
| 2 |
5
| ||
| 2 |
点评:本题考查的是切线的性质及相似三角形的判定与性质、全等三角形的判定与性质,待定系数法求一次函数的解析式,涉及面较广,难度较大.

练习册系列答案
相关题目
下列各组数据中,可以构成直角三角形三边长的是( )
| A、5,6,7 |
| B、40,41,7 |
| C、7,24,25 |
| D、2,3,4 |
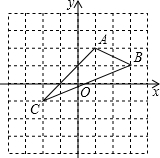 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1). 在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图1、图2中的△ABC和△DEF都是格点三角形.
在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图1、图2中的△ABC和△DEF都是格点三角形.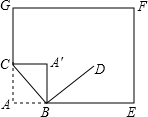 如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.
如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数. 在矩形ABCD中,点E,F在边DC上,EF=10米,点G在AB上,AG=52米,若∠EAB=36°,∠FGB=72°,求BC的长(精确到个位).
在矩形ABCD中,点E,F在边DC上,EF=10米,点G在AB上,AG=52米,若∠EAB=36°,∠FGB=72°,求BC的长(精确到个位).