题目内容
6.下列各式$\frac{1}{5}$(1-x)=0,$\frac{{4{x^2}}}{π-3}$=0,$\frac{{{x^2}-{y^2}}}{2}$=0,$\frac{1}{x}+x=0$,x2+3x=0,其中一元二次方程的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 利用一元二次方程的定义分别分析得出答案.
解答 解:$\frac{1}{5}$(1-x)=0.是一元一次方程,不合题意;
$\frac{{4{x^2}}}{π-3}$=0,是一元二次方程,符合题意;
$\frac{{{x^2}-{y^2}}}{2}$=0,含有两个未知数,不是一元二次方程,
$\frac{1}{x}$+x=0,不符合一元二次方程的定义,
x2+3x=0,是一元二次方程,符合题意,
故其中一元二次方程的个数为:2.
故选:A.
点评 此题主要考查了一元二次方程的定义,正确把握一元二次方程具备的条件是解题关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 (1)在平面直角坐标系中,点A的坐标是(0,2).在x轴上任取一点M,完成下列作图步骤:
(1)在平面直角坐标系中,点A的坐标是(0,2).在x轴上任取一点M,完成下列作图步骤: 已知:如图,M、N分别是?ABCD的对边中点,且AD=2AB,求证:PMQN为矩形.
已知:如图,M、N分别是?ABCD的对边中点,且AD=2AB,求证:PMQN为矩形.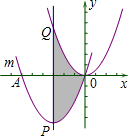 如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,且抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q.
如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,且抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q. 已知:如图,在△ABC中,AB=AC,BD是AC边上的高,点P是边BC上的任意一点,PE⊥AB,PF⊥AC,垂足分别为E、F.
已知:如图,在△ABC中,AB=AC,BD是AC边上的高,点P是边BC上的任意一点,PE⊥AB,PF⊥AC,垂足分别为E、F.