题目内容
16.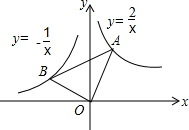 如图,在x轴的上方,∠BOA(直角)绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则△AOB面积的最小值为$\sqrt{2}$.
如图,在x轴的上方,∠BOA(直角)绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则△AOB面积的最小值为$\sqrt{2}$.
分析 过点B、A作x轴的垂线,垂足分别为点C、D,再过点B作AD的垂线,交AD于点E,则四边形BCDE为矩形.设点B的坐标为(m,$\frac{1}{m}$),点A的坐标为(n,$\frac{2}{n}$),利用勾股定理可用n、m表示OB、OA、AB的长,再利用三角函数证明∠OAB为一定值,即tan$∠OAB=\frac{OB}{OA}=\frac{\sqrt{2}}{2}$,利用这个关系及不等关系a2+b2≥2ab可求出△AOB面积的最小值.
解答 解:如图所示:过点B、A作x轴的垂线,垂足分别为点C、D,再过点B作AD的垂线,交AD于点E.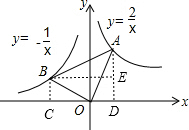
∵BC⊥OC,AD⊥OD,BE⊥AD,
∴四边形BCDE是矩形,
∵点B、A分别在函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$上,
∴设点B的坐标为(m,$\frac{1}{m}$),点A的坐标为(n,$\frac{2}{n}$),
∴OC=-m,BC=-$\frac{1}{m}$,OD=n,AD=$\frac{2}{n}$,BE=n-m,AE=$\frac{2}{n}+\frac{1}{m}$,
∴根据勾股定理,在Rt△OBC、Rt△ODA、Rt△ABE中,可分别求出:
OB=$\sqrt{B{C}^{2}+O{C}^{2}}$=$\sqrt{{m}^{2}+\frac{1}{{m}^{2}}}$
OA=$\sqrt{A{D}^{2}+O{D}^{2}}$=$\sqrt{{n}^{2}+\frac{4}{{n}^{2}}}$,
AB=$\sqrt{B{E}^{2}+A{E}^{2}}$=$\sqrt{(n-m)^{2}+(\frac{2}{n}+\frac{1}{m})^{2}}$=$\sqrt{{{m}^{2}+\frac{1}{{m}^{2}}+n}^{2}+\frac{4}{{n}^{2}}-2mn+\frac{4}{mn}}$,
又∵∠AOB是直角,
∴在Rt△AOB中,AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{m}^{2}+\frac{1}{{m}^{2}}+{n}^{2}+\frac{4}{{n}^{2}}}$,
即:=$\sqrt{{{m}^{2}+\frac{1}{{m}^{2}}+n}^{2}+\frac{4}{{n}^{2}}-2mn+\frac{4}{mn}}$=$\sqrt{{m}^{2}+\frac{1}{{m}^{2}}+{n}^{2}+\frac{4}{{n}^{2}}}$,
∴$\frac{4}{mn}-2mn=0$
∴mn=-$\sqrt{2}$
即:m=-$\frac{\sqrt{2}}{n}$
在Rt△AOB中,tan∠OAB=$\frac{OB}{OA}$=$\frac{\sqrt{{m}^{2}+\frac{1}{{m}^{2}}}}{\sqrt{{n}^{2}+\frac{4}{{n}^{2}}}}$=$\frac{\sqrt{\frac{2}{{n}^{2}}+\frac{{n}^{2}}{2}}}{\sqrt{{n}^{2}+\frac{4}{{n}^{2}}}}$=$\frac{\sqrt{2}}{2}$,
∴∠OAB 的大小不变,即$\frac{OB}{OA}$的值不变,OB=$\frac{\sqrt{2}}{2}$OA
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$•$\frac{\sqrt{2}}{2}$•OA2=$\frac{\sqrt{2}}{4}$(n2+$\frac{4}{{n}^{2}}$),
∵n2+$\frac{4}{{n}^{2}}$≥4
∴S△AOB≥$\frac{\sqrt{2}}{4}$×4=$\sqrt{2}$
即:△AOB面积的最小值为$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查了反比例函数系数k的几何意义、坐标与图形变化-旋转,关键是弄清楚在整个旋转变化的过程中存在的不变关系.

 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | 16×10-7 | B. | 1.6×10-6 | C. | 1.6×10-5 | D. | 16×10-5 |
| A. | 点P在圆内 | B. | 点P在圆上 | C. | 点P在圆外 | D. | 不能确定 |
| A. | 2 013 | B. | -2 013 | ||
| C. | 2 013或-2 013 | D. | 1 006.5或-1 006.5 |