题目内容
5.一次函数y=2x-4的图象与两坐标轴交点的距离是( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
分析 分别求出直线y=2x-4于坐标轴的交点A、B两点的坐标,再根据勾股定理求解即可
解答 解:∵一次函数y=2x-4的图象与坐标轴交于A、B两点,
∴A(0,-4),B(2,0),
∴OA=4,OB=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}=\sqrt{{4}^{2}+{2}^{2}}=2\sqrt{5}$,
故选B
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
15.下列多项式中,能用公式法分解因式的是( )
| A. | -m2+n2 | B. | a2-2ab-b2 | C. | m2+n2 | D. | -a2-b2 |
16.不等式组$\left\{\begin{array}{l}{x<-2}\\{x>-3}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x<-2 | C. | -3<x<-2 | D. | 无解 |
20.若$\sqrt{a-5}$在实数范围内有意义,则a的取值范围是( )
| A. | a>0 | B. | a>5 | C. | a≥5 | D. | a≤5 |
10.下列计算正确的是( )
| A. | x3•x2=x5 | B. | x5÷x=x3 | C. | (x2)3=x5 | D. | (3x)2=6x2 |
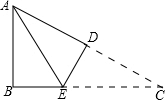 如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.
如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.