题目内容
3.曾好妈妈在淘宝网开店,经销一种文具,每件成本是4元,每件售价6元,年销售量为10万件,为了获得更好的效益,曾好妈妈决定拿出一笔资金做广告,根据经验,每年投入的广告费是x(万元)时,产品的年销售量将是原销售量的y倍,且y是x的二次函数,他们的关系如下表:| x(万元) | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
(2)如果把利润看作是销售额减去成本费和广告费,试写出年利润S(万元)与广告费x(万元)的函数关系式;(销售额=售价×销售量)
(3)如果投入的广告费为1-5万元,问广告费在什么范围内,曾好妈妈所获年利润随广告费的增加而增加?
分析 (1)根据题意可以设出y与x的函数关系式,根据表格中的数据可以求得y与x的函数关系式中的各个系数,从而可以求得y与x的函数关系式;
(2)根据题意可以写出年利润S(万元)与广告费x(万元)的函数关系式;
(3)将第二问中关系式化为顶点式,即可得到如果投入的广告费为1-5万元,广告费在什么范围内,曾好妈妈所获年利润随广告费的增加而增加.
解答 解:(1)设y与x的函数关系式是y=ax2+bx+c,
由表格可得,
$\left\{\begin{array}{l}{c=1}\\{a+b+c=1.5}\\{4a+2b+c=1.8}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=-0.1}\\{b=0.6}\\{c=1}\end{array}\right.$
即y与x的函数关系式是y=-0.1x2+0.6x+1;
(2)由题意可得,
S=(6-2)×10y-x=4×10(-0.1x2+0.6x+1)-x=-4x2+23x+40,
即年利润S(万元)与广告费x(万元)的函数关系式是S=-4x2+23x+40;
(3)S=-4x2+23x+40=$-4(x-\frac{23}{8})^{2}+\frac{1169}{11}$,
∵-4<0,
∴函数S在x≤$\frac{23}{8}$时,S随x的增大而增大;函数S在x≥$\frac{23}{8}$时,S随x的增大而减小;
∵1≤x≤5,
∴在1≤x≤$\frac{23}{8}$时,S随着x的增大而增大,
即投入的广告费为1-5万元,广告费在1≤x≤$\frac{23}{8}$范围内,曾好妈妈所获年利润随广告费的增加而增加.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出题目中的等量关系,列出相应的函数解析式,会求函数的解析式,并将函数解析可以化为顶点式,会求函数的最值,明确函数的增减性.

 阅读快车系列答案
阅读快车系列答案| A. | m≠0 | B. | m>2 | C. | m=1 | D. | m=2 |
| A. | 3楼6号 | B. | 南大街27号 | ||
| C. | 北偏东60° | D. | 东经120°,北纬37° |
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 无数个 |
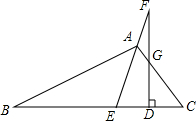 如图,在△ABC中,AE是△ABC的角平分线,在EA的延长线上取一点F,作FD⊥BC于点D,若∠B=36°,∠C=64°,则∠EFD的度数为( )
如图,在△ABC中,AE是△ABC的角平分线,在EA的延长线上取一点F,作FD⊥BC于点D,若∠B=36°,∠C=64°,则∠EFD的度数为( )| A. | 10° | B. | 12° | C. | 14° | D. | 16° |

 如图,在Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B且S△ABO=1.5.
如图,在Rt△ABO中,顶点A是双曲线y=$\frac{k}{x}$与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B且S△ABO=1.5.