题目内容
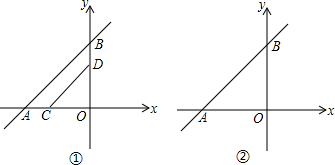
如图,已知直线y=x+8与x轴、y轴分别交于点A、B.线段AO上的一个动点C从A出发以每秒1个单位的速度沿A→O移动(C与A,O不重合),果C作CD∥AB,交y轴于点D,将四边形ACDB沿CD对折,可得四边形CEFD,设点C的运动时间为t秒.
(1)直线y=x+8与坐标轴的交点坐标是A ,B .
(2)在图①中画出四边形ACDB沿CD对折后的图形(不写画法).
(3)若EF交x轴于G点,求证:四边形CGFD为平行四边形;并求t为何值时,四边形CGFD为菱形(计算结果不需要化简).
(4)设四边形DCEF落在第三象限内的图形面积为S,求S关于t的函数表达式,并求出S的最大值.
(1)直线y=x+8与坐标轴的交点坐标是A
(2)在图①中画出四边形ACDB沿CD对折后的图形(不写画法).
(3)若EF交x轴于G点,求证:四边形CGFD为平行四边形;并求t为何值时,四边形CGFD为菱形(计算结果不需要化简).
(4)设四边形DCEF落在第三象限内的图形面积为S,求S关于t的函数表达式,并求出S的最大值.

考点:一次函数综合题
专题:
分析:(1)根据自变量与函数值的对应关系,可得图象与坐标轴的交点坐标;
(2)根据轴对称的性质,可得轴对称图形;
(3)根据对应线段平行于对称轴,可得EF与CD的关系,根据等腰直角三角形的性质,可得∠ABO,根据平行线的性质,可得∠CDO,根据邻补角,可得∠BDC,再根据轴对称的性质,可得∠CDF,根据角的和差,可得∠BDF,根据平行四边形的判定,可得CGFD为平行四边形;根据等腰梯形的判定,可得BD与AC的关系,根据轴对称的性质,可得DF的长,根据勾股定理,可得CD的长,根据菱形的判定,可得答案;
(4)分类讨论:当0<t≤4时,根据三角形的面积公式,可得函数解析式,根据二次函数的性质,可得答案;当4<t<8时,根据面积的和差,可得函数解析式,根据二次函数的性质,可得答案.
(2)根据轴对称的性质,可得轴对称图形;
(3)根据对应线段平行于对称轴,可得EF与CD的关系,根据等腰直角三角形的性质,可得∠ABO,根据平行线的性质,可得∠CDO,根据邻补角,可得∠BDC,再根据轴对称的性质,可得∠CDF,根据角的和差,可得∠BDF,根据平行四边形的判定,可得CGFD为平行四边形;根据等腰梯形的判定,可得BD与AC的关系,根据轴对称的性质,可得DF的长,根据勾股定理,可得CD的长,根据菱形的判定,可得答案;
(4)分类讨论:当0<t≤4时,根据三角形的面积公式,可得函数解析式,根据二次函数的性质,可得答案;当4<t<8时,根据面积的和差,可得函数解析式,根据二次函数的性质,可得答案.
解答:解:(1)(-8,0),(0,8);
(2)如图1:
 ;
;
四边形CEFD即为四边形ACDB沿CD对折后的图形,
(3)∵四边形CEFD与四边形ACDB关于直线CD对称,CD∥AB,
∴EF∥CD.
∵OA=OB,∠AOB=90°,
∴∠ABO=45°,
∵AB∥CD,
∴∠CDB=135°.∠CDF=∠CDB=135°.∠BDF=360°-2×135°,即DF⊥y轴,
∴DF∥CG,
∴四边形CGFD是平行四边形.
如图2,要使四边形CGFD为菱形,只需CD=DF.

∵AB∥CD,∠CAB=∠DBA,
∴AC=BD.
∴DF=BD=AC=t.
又∵OC=OD=8-t,
∴CD=
(8-t).
∴
(8-t)=t.
∴t=
=16-8
,
当t=16-8
时,四边形CGFD为菱形;
(4)分两种情况讨论:
①当0<t≤4时,四边形CEFD落在第三象限内的图形是△CEG,
∴S=
t2,∵S=
t2在t>0时,S随t的增大而增大,
∴当t=4时,S最大=
×42=8;
②当4<t<8时,如图3,
 ,
,
四边形CEFD落在第三象限内的图形是CEHO,其中H为EF与y轴的交点,
CG=CE=t,CO=8-t,OG=OH=t-(8-t)=2t-8,
∴S四边形COHE=S△CEG-S△OGH
S=
t2-
(2t-8)2=-
t2+16t-32=-
(t-
)2+
,
∵a=-
<0,
∴S有最大值,
当t=
时,S最大=
.
(2)如图1:
 ;
;四边形CEFD即为四边形ACDB沿CD对折后的图形,
(3)∵四边形CEFD与四边形ACDB关于直线CD对称,CD∥AB,
∴EF∥CD.
∵OA=OB,∠AOB=90°,
∴∠ABO=45°,
∵AB∥CD,
∴∠CDB=135°.∠CDF=∠CDB=135°.∠BDF=360°-2×135°,即DF⊥y轴,
∴DF∥CG,
∴四边形CGFD是平行四边形.
如图2,要使四边形CGFD为菱形,只需CD=DF.

∵AB∥CD,∠CAB=∠DBA,
∴AC=BD.
∴DF=BD=AC=t.
又∵OC=OD=8-t,
∴CD=
| 2 |
∴
| 2 |
∴t=
8
| ||
1+
|
| 2 |
当t=16-8
| 2 |
(4)分两种情况讨论:
①当0<t≤4时,四边形CEFD落在第三象限内的图形是△CEG,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴当t=4时,S最大=
| 1 |
| 2 |
②当4<t<8时,如图3,
 ,
,四边形CEFD落在第三象限内的图形是CEHO,其中H为EF与y轴的交点,
CG=CE=t,CO=8-t,OG=OH=t-(8-t)=2t-8,
∴S四边形COHE=S△CEG-S△OGH
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 16 |
| 3 |
| 32 |
| 3 |
∵a=-
| 3 |
| 2 |
∴S有最大值,
当t=
| 16 |
| 3 |
| 32 |
| 3 |
点评:本题考查了一次函数综合题,(1)利用了自变量与函数值的对应关系;(2)利用了轴对称的性质;(3)利用了等腰直角三角形的性质,平行四边形的判定,菱形的判定;(3)利用了三角形面积公式,面积的和差,二次函数的性质,利用知识点多综合性较强.

练习册系列答案
相关题目
以下四个语句中,错误的是( )
| A、两点确定一条直线 |
| B、0.1°=6′ |
| C、最大的负整数是-1 |
| D、射线AB与射线BA是同一条射线 |
 如图的立体图形可由哪个平面图形绕轴旋转而成( )
如图的立体图形可由哪个平面图形绕轴旋转而成( )A、 |
B、 |
C、 |
D、 |
 如图,已知点C是线段AB的中点,D是BC上一点,E是DB的中点,若CE=4cm,AD=
如图,已知点C是线段AB的中点,D是BC上一点,E是DB的中点,若CE=4cm,AD= 小昆和小明玩摸牌游戏,游戏规则如下,有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌子上,随机抽出一张,记下牌面数字,再从剩下的牌中抽出一张,两次抽到的牌分别记为A、B.
小昆和小明玩摸牌游戏,游戏规则如下,有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌子上,随机抽出一张,记下牌面数字,再从剩下的牌中抽出一张,两次抽到的牌分别记为A、B.