题目内容
6.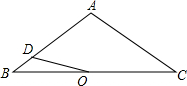 如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )
如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )| A. | 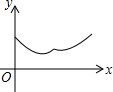 | B. | 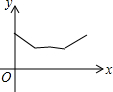 | C. | 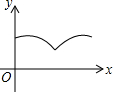 | D. | 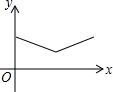 |
分析 作OE⊥AB,根据等腰三角形的性质和勾股定理表示出DE、OD、OE,当0<x≤4时,根据勾股定理表示出y2,即可判断图象.
解答 解:如图,作OE⊥AB,
∵点O是BC中点,AB=AC=4,∠BAC=120°.
∴AO=2,BO=2$\sqrt{3}$,OE=$\sqrt{3}$,BE=3,
设BD=x,OD=y,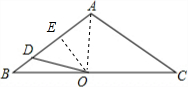
∴DE=3-x,
在Rt△ODE中,
DE2+OE2=OD2,
∴y2=(3-x)2+($\sqrt{3}$)2
整理得:y2=x2-6x+12,
当0<x≤4时,y2=x2-6x+12,函数的图象呈抛物线并开口向上,
故选:A.
点评 本题考查了动点问题的函数图象,根据图形运用数形结合列出函数表达式是解决问题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
16.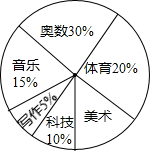 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
(1)七年级共有学生360人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 36 | 54 | 18 |
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
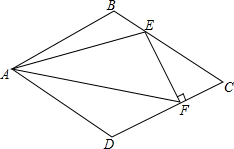 菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.
菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.
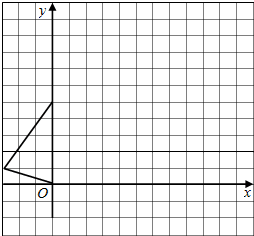 如图,已知△OAB的三个顶点的坐标分别为O(0,0)、A(-3,1)、B(0,5),三角形内有任意一点P坐标为(a,b)
如图,已知△OAB的三个顶点的坐标分别为O(0,0)、A(-3,1)、B(0,5),三角形内有任意一点P坐标为(a,b)