题目内容
1.等腰△ABC中,CA=CB,点D为边AB上一点,沿CD折叠△CAD得到△CFD,边CF交边AB于点E,CD=CE,连接BF.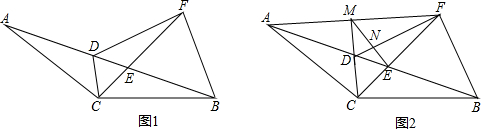
(1)求证:FD=FB.
(2)连接AF交CD的延长线于点M,连接ME交线段DF于点N,若EF=4EC,AB=22,求MN的长.
分析 (1)首先根据全等三角形判定的方法,判断出△ACE≌△BCD,推得AE=BD,DF=EB,然后判断出△DCF≌△ECB,推得∠FDE=∠BCE,最后根据相似三角形判定的方法,判断出△DEF∽△CEB,推得$\frac{DE}{EF}$=$\frac{CE}{EB}$,再根据∠DEC=∠FEB,推得△DEC∽△FEB,再判断出∠FDB=∠FBD,即可推得FD=FB.
(2)首先根据相似三角形判定的方法,判断出△DEF∽△CEB,推得$\frac{ED}{CE}=\frac{EF}{EB}$,再判断出△CED∽△BEF,推得∠DCE=∠EBF,进而判断出△EBF、△BCF为等腰三角形,所以∠BCF=∠EBF,∠DCE=∠BCF,CE为△BCD和∠BCD的平分线;最后由角平分线定理,可得$\frac{CB}{CD}=\frac{EB}{ED}$,$\frac{CE+EF}{CE}=\frac{EB}{ED}$,求出ED、EC的值各是多少;再判断出△MNG∽△END,推得$\frac{MG}{ED}$=$\frac{MN}{EN}$,$\frac{MN}{EN}$=$\frac{5}{2}$,MN=$\frac{5}{7}$ME,在△MCE中,由余弦定理,可得ME2=MC2+EC2-2MC×EC×cos∠DCE,ME2=10EC2-3.6EC2=6.4EC2,据此求出MN的大小即可.
解答 (1)证明:如图1,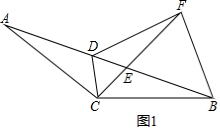 ,
,
∵CA=CB,
∴∠A=∠ABC,
∵CD=CE,
∴∠CDE=∠CED,
在△ACE与△BCD中
$\left\{\begin{array}{l}{∠A=∠ABC}\\{∠AEC=∠BDC}\\{AC=CB}\end{array}\right.$
∴△ACE≌△BCD(AAS)
∴AE=BD,
∴AD=EB,
∵AD=DF,
∴DF=EB,
在△DCF与△ECB中
$\left\{\begin{array}{l}{DF=EB}\\{CF=CB}\\{CD=CE}\end{array}\right.$
∴△DCF≌△ECB(SSS),
∠DCE=∠ECB,∠DFE=∠EBC,
∴∠FDE=∠BCE,
∴△DEF∽△CEB,
∴$\frac{DE}{EF}$=$\frac{CE}{EB}$,
∵∠DEC=∠FEB,
∴△DEC∽△FEB,
∴∠DCE=∠EBF,
∴∠FDB=∠FBD,
∴FD=FB.
(2)解:∵沿CD折叠△CAD得到△CFD,
∴CA=CF,∠CAD=∠CFD,
∵∠CAD=∠CBE,
∴∠CFD=∠CBE,
∵∠DEF=∠CEB,
∴△DEF∽△CEB,
∴$\frac{ED}{CE}=\frac{EF}{EB}$,
又∵∠CED=∠BEF,
∴△CED∽△BEF,
∴∠DCE=∠EBF,
∵CD=CE,
∴BE=BF,△EBF为等腰三角形,
∵CF=CB,
∴△BCF为等腰三角形,
则∠BCF=∠EBF,
∴∠DCE=∠BCF,CE为△BCD和∠BCD的平分线,
由角平分线定理,可得
$\frac{CB}{CD}=\frac{EB}{ED}$,$\frac{CE+EF}{CE}=\frac{EB}{ED}$,
∵EF=4EC,
∴$\frac{EB}{ED}$=5,
∵AB=AD+ED+EB=22,
∴5ED+ED+5ED=22,
解得ED=2,
∵$\frac{ED}{CE}=\frac{EF}{EB}$,
∴4CE2=5ED2,EC=$\sqrt{5}$,
由余弦定理,可得
ED2=CD2+CE2-2CD×CEcos∠DCE,cos∠DCE=$\frac{3}{5}$.
如图2,过点M作AE的平行线分别交FD、EF于点G、H, ,
,
∵M为AF边的中点,
∴点G、H是FD、EF的中点,
∵EF=4EC,
∴EH=2EC,
∴MD=2CD,MH=3ED,
∵GH=$\frac{1}{2}$ED,
∴MG=$\frac{5}{2}$ED,
∵△MNG∽△END,
∴$\frac{MG}{ED}$=$\frac{MN}{EN}$,$\frac{MN}{EN}$=$\frac{5}{2}$,MN=$\frac{5}{7}$ME,
在△MCE中,由余弦定理,可得
ME2=MC2+EC2-2MC×EC×cos∠DCE,
ME2=10EC2-3.6EC2=6.4EC2,
∴ME=4$\sqrt{2}$,MN=$\frac{20\sqrt{2}}{7}$.
点评 (1)此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

| A. | (a-b)2=-(b-a)2 | B. | $\frac{1}{{x}^{3}}$=x-3 | C. | $\frac{{a}^{2}+1}{a+1}$=a+1 | D. | x6÷x2=x3 |
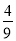 B.
B. 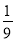 C.
C. 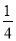 D.
D. 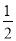
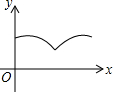
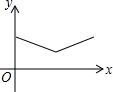
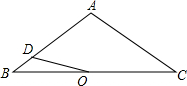 如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )
如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )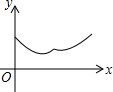
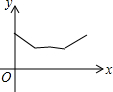
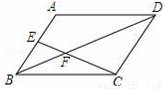
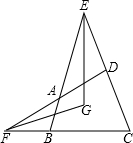 如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.
如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADC=60°,∠ABC=80°.