题目内容
11.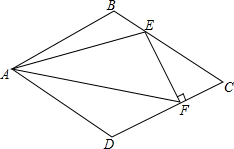 菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.
菱形ABCD的边长为1,∠C=60°,E、F分别在BC、CD上,且EF⊥CD,则△AEF面积的最大值为$\frac{\sqrt{3}}{4}$.
分析 设CF=x,则DF=1-x,CE=2x,BE=1-2x,可知0<x≤$\frac{1}{2}$,计算出设S1=S△ADF+S△ABE+S△CEF=$\frac{\sqrt{3}}{4}$(2x2-3x+2),(0<x≤$\frac{1}{2}$),根=$\frac{\sqrt{3}}{4}$(2x2-3x+2)(据当x=$\frac{1}{2}$时,S1由最小值为$\frac{\sqrt{3}}{4}$,根据S△AEF=S菱形ABCD-(S△ADF+S△ABE+S△CEF),所以S△AEF的最大值=${S}_{菱形ABCD}-\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{4}$.
解答 解:设CF=x,则DF=1-x,
∵∠C=60°,且EF⊥CD,
∴∠CEF=30°,
∴CE=2x,
∴BE=1-2x,
可知0<x≤$\frac{1}{2}$,
∵菱形ABCD中,∠C=60°,
∴∠B=∠D=120°,
设S1=S△ADF+S△ABE+S△CEF
=$\frac{1}{2}$AD•DF•sin∠D+$\frac{1}{2}$AB•BE•sin∠B+$\frac{1}{2}$CE•CFsin∠C
=$\frac{1}{2}$×1×(1-x)×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×1×(1-2x)×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×2x•x×$\frac{\sqrt{3}}{2}$
=$\frac{\sqrt{3}}{4}$(2x2-3x+2)(0<x≤$\frac{1}{2}$)
∴当x=$\frac{1}{2}$时,S1由最小值为$\frac{\sqrt{3}}{4}$,
∵S△AEF=S菱形ABCD-(S△ADF+S△ABE+S△CEF)
∴S△AEF的最大值=${S}_{菱形ABCD}-\frac{\sqrt{3}}{4}$=2×$\frac{1}{2}$×1×1×$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题考查菱形的性质,解决本题的关键是求出S△ADF+S△ABE+S△CEF的最小值,即可求出△AEF面积的最大值.

 若P、Q是线段AB上的两个黄金分割点,且PQ=2$\sqrt{5}$-4,则AB=2.
若P、Q是线段AB上的两个黄金分割点,且PQ=2$\sqrt{5}$-4,则AB=2.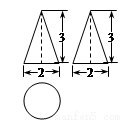
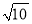 π C.
π C. 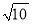 π D. 3π
π D. 3π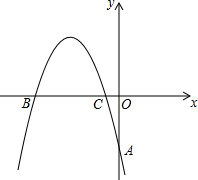 如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4),B(x1,0),C(x2,0)三点,且|x2-x1|=5.
如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c,经过A(0,-4),B(x1,0),C(x2,0)三点,且|x2-x1|=5.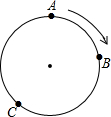 上海世博园中,有A、B、C三个国家的展馆由一个圆形通道相连,小明在参观游览过程中发现,沿顺时针方向走,从A馆到C馆要12分钟,从B馆到A馆要15分钟,从C馆到B馆要11分钟,你能求出从A馆到B馆需要多少分钟吗?
上海世博园中,有A、B、C三个国家的展馆由一个圆形通道相连,小明在参观游览过程中发现,沿顺时针方向走,从A馆到C馆要12分钟,从B馆到A馆要15分钟,从C馆到B馆要11分钟,你能求出从A馆到B馆需要多少分钟吗? ,
,  ,
,  ,请用“<”把a、b、c连起来__________。
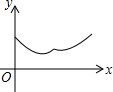
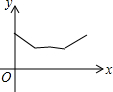
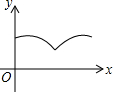
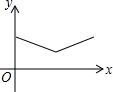
,请用“<”把a、b、c连起来__________。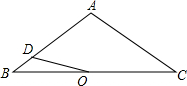 如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )
如图,△ABC中,AB=AC=4,∠BAC=120°.点O是BC中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为x,OD长为y.则函数y的图象大致为( )