题目内容
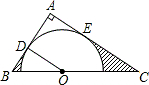 如图,在△ABC中,∠A=90°,O是BC边上的一点,以点O为圆心的分分别与边AB,AC相切于点D,E连接OD,已知BD=2,AD=3.求阴影部分的面积.
如图,在△ABC中,∠A=90°,O是BC边上的一点,以点O为圆心的分分别与边AB,AC相切于点D,E连接OD,已知BD=2,AD=3.求阴影部分的面积.考点:扇形面积的计算,切线的性质
专题:
分析:连接OE,得到∠ADO=∠AEO=90°,根据∠A=90°,推出矩形ADOE,进一步推出正方形ADOE,得出OD∥AC,OD=AD=3,∠BOD=∠C,即可求出tanC=
;设⊙O与BC交于M、N两点,由四边形ADOE是正方形,推出∠COE+∠BOD=90°,根据tanC=
,OE=3,求出EC=
,根据S扇形DOM+S扇形EON=S扇形DOE,即可求出阴影部分的面积.
| 2 |
| 3 |
| 2 |
| 3 |
| 9 |
| 2 |
解答: 解:如图,连接OE,设⊙O与BC交于M、N两点,
解:如图,连接OE,设⊙O与BC交于M、N两点,
∵AB、AC分别切⊙O于D、E两点,
∴AD⊥OD,AE⊥OE,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中,tan∠BOD=
,
∴tanC=
.
∵四边形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中,tanC=
=
,OE=3,
∴EC=
,
∴S扇形DOM+S扇形EON=S扇形DOE=
S圆O=
π×32=
π,
∴S阴影=S△BOD+S△COE-(S扇形DOM+S扇形EON)=
,
答:图中两部分阴影面积的和为
.
 解:如图,连接OE,设⊙O与BC交于M、N两点,
解:如图,连接OE,设⊙O与BC交于M、N两点,∵AB、AC分别切⊙O于D、E两点,
∴AD⊥OD,AE⊥OE,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中,tan∠BOD=
| BD |
| OD |
∴tanC=
| 2 |
| 3 |
∵四边形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中,tanC=
| 2 |
| 3 |
| OE |
| EC |
∴EC=
| 9 |
| 2 |
∴S扇形DOM+S扇形EON=S扇形DOE=
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
∴S阴影=S△BOD+S△COE-(S扇形DOM+S扇形EON)=
| 39 |
| 4 |
答:图中两部分阴影面积的和为
| 39 |
| 4 |
点评:本题主要考查对正方形的性质和判定,锐角三角函数的定义,扇形的面积,切线的性质等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目
目前全球海洋面积约为36100万平方公里,用科学记数法将数36100万表示为( )
| A、3.61×108 |
| B、361×106 |
| C、3.61×104 |
| D、361×102 |
已知小球从点A运动到点B,速度v(米/秒)是时间t(秒)的正比例函数,3秒时小球的速度是6米/秒,那么速度v与时间t之间的关系式是( )
A、v=
| ||
B、v=
| ||
| C、v=3t | ||
| D、v=2t |