题目内容
6.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=12,CD=14,把三角板DEC绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与 CD1交于点O,则线段AD1的长度为10.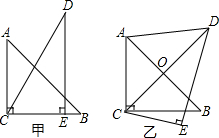
分析 首先由旋转的角度为15°,可知∠ACD1=45°.已知∠CAO=45°,即可得AO⊥CD1,然后可在Rt△AOC和Rt△AOD1中,通过解直角三角形求得AD1的长.
解答 解:由题意易知:∠CAB=45°,∠ACD=30°.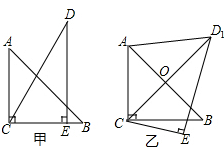
若旋转角度为15°,则∠ACO=30°+15°=45°.
∴∠AOC=180°-∠ACO-∠CAO=90°.
在等腰Rt△ABC中,AB=12,则AC=BC=6$\sqrt{2}$.
同理可求得:AO=OC=6.
在Rt△AOD1中,OA=6,OD1=CD1-OC=8,
由勾股定理得:AD1=10.
故答案为:10.
点评 此题主要考查了旋转的性质以及解直角三角形的综合应用,能够发现AO⊥OC是解决此题的关键.

练习册系列答案
相关题目
6.不等式3x≤2(x-1)的解集为( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤-2 | D. | x≥-2 |
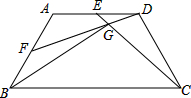 如图,已知:在梯形ABCD中,AD∥BC,∠A=120°,AB=AD=CD,点E、点F分别为线段AD、AB的中点,连接CE、DF,CE与DF相交于点G,连接BG.若DG=2,则线段BG的长为2$\sqrt{13}$.
如图,已知:在梯形ABCD中,AD∥BC,∠A=120°,AB=AD=CD,点E、点F分别为线段AD、AB的中点,连接CE、DF,CE与DF相交于点G,连接BG.若DG=2,则线段BG的长为2$\sqrt{13}$.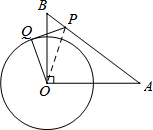 如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )


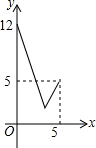
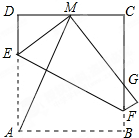 将边长为5正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.
将边长为5正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.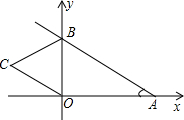 如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.
如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.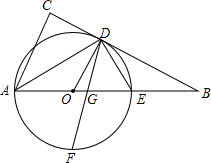 如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG
如图,E是△ABC的边AB上一点,以AE为直径的⊙O经过BC上的一点D,且OD∥AC,∠ADE的平分线DF交AB于G,交⊙O于F,且BD=BG