题目内容
8.用配方法解方程2y2+3=7y,配方后得( )| A. | (y+$\frac{7}{4}$)2=$\frac{25}{16}$ | B. | (y-$\frac{7}{4}$)2=$\frac{25}{16}$ | C. | (y+$\frac{7}{2}$)2=$\frac{25}{16}$ | D. | (y-$\frac{7}{2}$)2=$\frac{25}{16}$ |
分析 整理成2y2-7y=-3,将二次项系数化为1后配上一次项系数一半的平方可得.
解答 解:原方程整理可得:2y2-7y=-3,
∴y2-$\frac{7}{2}$y=-$\frac{3}{2}$,
∴y2-$\frac{7}{2}$y+$\frac{49}{16}$=-$\frac{3}{2}$+$\frac{49}{1}$,即(y-$\frac{7}{4}$)2=$\frac{25}{16}$,
故选:B.
点评 本题主要考查配方法解一元二次方程,熟练掌握配方法解一元二次方程的基本步骤是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.学校举行广播操比赛,八年级三个班的各项得分及三项得分的平均数如下(单位:分).
根据表中信息回答下列问题:
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
| 服装统一 | 进退场有序 | 动作规范 | 动作整齐 | |
| 一班 | 80 | 84 | 88 | 84 |
| 二班 | 97 | 78 | 80 | 85 |
| 三班 | 90 | 78 | 84 | 84 |
(1)学校将“服装统一”、“队形整齐”、“动作规范”三项按2:3:5的比例计算各班成绩,求八年级三个班的成绩;
(2)由表中三项得分的平均数可知二班排名第一,在(1)的条件下,二班成绩的排名发生了变化,请你说明二班成绩排名发生变化的原因.
19.己知一次函数y=kx+b的图象经过第一、二、四象限,则b的值可能是( )
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
13.某事件发生的概率为$\frac{1}{4}$,则下列说法不正确的是( )
| A. | 无数次实验后,该事件发生的频率逐渐稳定在$\frac{1}{4}$左右 | |
| B. | 无数次实验中,该事件平均每4次出现1次 | |
| C. | 每做4次实验,该事件就发生1次 | |
| D. | 逐渐增加实验次数,该事件发生的频率就和$\frac{1}{4}$逐渐接近 |
20. 数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
 数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )
数轴上的A,B,C,D四个点中,离表示-$\sqrt{2}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
17.若分式$\frac{3}{x+3}$在实数范围内有意义,则x的取值范围是( )
| A. | x<-3 | B. | x>-3 | C. | x≠-3 | D. | x=-3 |
 请画出由五个正方体组成的如图所示物体的三视图.
请画出由五个正方体组成的如图所示物体的三视图.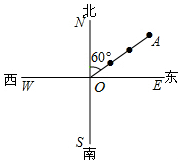 如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.
如图,货轮O在航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C,按下列要求画出.