题目内容
7.已知a≠b,且a、b满足a2-3a-4=0,b2-3b-4=0,那么$\frac{a}{b}$+$\frac{b}{a}$的值等于-$\frac{17}{4}$.分析 由a、b满足a2-3a-4=0、b2-3b-4=0,可得出a、b是方程x2-3x-4=0的两个根,利用根与系数的关系即可得出a+b=3、ab=-4,将$\frac{a}{b}$+$\frac{b}{a}$变形成$\frac{(a+b)^{2}-2ab}{ab}$,代入数据即可得出结论.
解答 解:∵a、b满足a2-3a-4=0,b2-3b-4=0,
∴a、b是方程x2-3x-4=0的两个根,
∴a+b=3,ab=-4,
∴$\frac{a}{b}$+$\frac{b}{a}$=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{{3}^{2}-2×(-4)}{-4}$=-$\frac{17}{4}$.
故答案为:-$\frac{17}{4}$.
点评 本题考查了根与系数的关系,根据根与系数的关系找出a+b=3、ab=-4是解题的关键.

练习册系列答案
相关题目
18.在同一段路上,某人上坡速度为a,下坡速度为b,则该人来回一趟的平均速度是( )
| A. | a | B. | b | C. | $\frac{a+b}{2}$ | D. | $\frac{2ab}{a+b}$ |
15.等腰三角形的周长为18cm,其中一边长为5cm,等腰三角形的底边长为( )
| A. | 5cm | B. | 6cm | C. | 5cm或8cm | D. | 8cm |
12.下列代数式:$\frac{b}{a}$、$\frac{x-y}{5}$、2π、x+1是单项式的有( ) 个.
| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
16.数轴上到-4的距离等于5个单位长度的点表示的数是( )
| A. | 5或-5 | B. | 1 | C. | -9 | D. | 1或-9 |
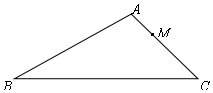 如图,在△ABC中,AB=8,AC=5,M是AC边上的一点,AM=2,在AB边上取一点N,使以A、M、N为顶点的三角形与△ABC相似,则AN的长为$\frac{16}{5}$或$\frac{5}{4}$.
如图,在△ABC中,AB=8,AC=5,M是AC边上的一点,AM=2,在AB边上取一点N,使以A、M、N为顶点的三角形与△ABC相似,则AN的长为$\frac{16}{5}$或$\frac{5}{4}$.