题目内容
17.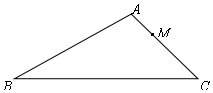 如图,在△ABC中,AB=8,AC=5,M是AC边上的一点,AM=2,在AB边上取一点N,使以A、M、N为顶点的三角形与△ABC相似,则AN的长为$\frac{16}{5}$或$\frac{5}{4}$.
如图,在△ABC中,AB=8,AC=5,M是AC边上的一点,AM=2,在AB边上取一点N,使以A、M、N为顶点的三角形与△ABC相似,则AN的长为$\frac{16}{5}$或$\frac{5}{4}$.
分析 根据相似三角形对应边成比例即可解答,由于没有确定三角形相似的对应角,故应分类讨论.
解答 解:分两种情况:
①△AMN∽△ABC,
∴AM:AB=AN:AC,
即2:8=AN:5,
∴AE=$\frac{5}{4}$;
②△AMN∽△ACB,
∴AM:AC=AN:AB,
即2:5=AN:8,
∴AE=$\frac{16}{5}$,
故答案为:$\frac{5}{4}$或$\frac{16}{5}$.
点评 本题考查了相似三角形的性质,对应边的比相等,注意分情况讨论是解决本题的关键.

练习册系列答案
相关题目
12.已知关于x的一元二次方程2x2-3kx+4=0的一个根是1,则k的值为( )
| A. | 4 | B. | 2 | C. | -2 | D. | -4 |
2.学校图书馆上周借书记录如表(超过50册的部分记为正,少于50册的部分记为负):
(1)上星期五借出图书多少册?
(2)上周平均每天借出图书为54册,问星期三最多借出多少册图书?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 0 | +8 | a | b | -7 |
(2)上周平均每天借出图书为54册,问星期三最多借出多少册图书?
9.下列各对数中,数值相等的一对是( )
| A. | -(-2)3和-23 | B. | (-3)2和-32 | C. | ($\frac{2}{3}$)2和$\frac{2^2}{3}$ | D. | |-32|和-(-32) |
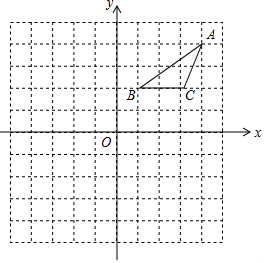 在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题;
在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题;