题目内容
5.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)在图1中,∠AOC=120°,∠BOC=60°.
(2)将图1中的三角板按图2的位置放置,使得OM在射线OA上,则∠CON=30°;
(3)将上述直角三角板按图3的位置放置,使得OM在∠BOC的内部,求∠BON-∠COM的度数.
分析 (1)点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,可以求得∠AOC和∠BOC的度数;
(2)根据∠AOC的度数和∠MON的度数可以得到∠CON的度数;
(3)根据∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,可以得到∠BON-∠COM的度数.
解答 解:(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°
故答案为:120°,60°;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC-∠MON=120°-90°=30°,
故答案为:30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON-∠BOM,∠COM=∠BOC-∠BOM,
则,∠BON-∠COM=90°-∠BOM-(60°-∠BOM)=30°,
即∠BON-∠COM的度数是30°.
点评 本题考查角的计算,解题的关键是找出各个角之间的关系,与已知条件建立关系,然后求出所求角的度数.

练习册系列答案
相关题目
16.下列调查中,适用普查方法的是( )
| A. | 了解一批袋装食品是否含有防腐剂 | |
| B. | 了解某班学生“50米跑”的成绩 | |
| C. | 了解江苏卫士“非诚勿扰”节目的收视率 | |
| D. | 调查我市冷饮市场雪糕质量情况 |
20.一次函数y=x+1和一次函数y=2x-2的图象的交点坐标是(3,4),据此可知方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x-y=2}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-4}\\{y=-3}\end{array}\right.$ |
10.利用墙的一边和长为39米的铁丝网,围成一个面积为180平方米的矩形,设这个矩形垂直于墙的一边长为x米,则根据题意可以列出正确的方程是( )
| A. | 2x2-39x+180=0 | B. | 2x2+39x+180=0 | C. | 2x2-39x-180=0 | D. | 2x2+39x-180=0 |
17.下列方程没有实数根的是( )
| A. | x2-x-1=0 | B. | x2-x+1=0 | C. | x2+x-1=0 | D. | x2-x=0 |
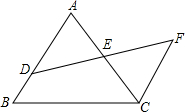 如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
 某球队14名队员的年龄统计如图所示,则球队队员的年龄的众数、中位数分别是17、16.
某球队14名队员的年龄统计如图所示,则球队队员的年龄的众数、中位数分别是17、16.