题目内容
3.已知a≠0,且满足(2a+1)(1-2a)-(3-2a)2+9a2=14a-7.求:(1)a2+$\frac{1}{{a}^{2}}$的值;
(2)$\frac{{a}^{2}}{3{a}^{4}+{a}^{2}+3}$的值.
分析 (1)根据已知条件求出a-$\frac{1}{a}$的值,然后利用完全平方公式解决.
(2)利用倒数法即可求解.
解答 解:(1)∵(2a+1)(1-2a)-(3-2a)2+9a2=14a-7,
∴1-4a2-9+12a-4a2+9a2=14a-7,
∴a2-2a-1=0
∵a≠0,
两边除以a得a-$\frac{1}{a}$=2,
∴a2-2+$\frac{1}{{a}^{2}}$=4,
∴a2+$\frac{1}{{a}^{2}}$=6.
(2)∵$\frac{3{a}^{4}+{a}^{2}+3}{{a}^{2}}$=3a2+1+$\frac{3}{{a}^{2}}$=3(a2+$\frac{1}{{a}^{2}}$)+1=3×6+1=19
∴$\frac{{a}^{2}}{3{a}^{4}+{a}^{2}+3}$=$\frac{1}{19}$.
点评 本题考查整式的化简、平方差公式、完全平方公式,学会用倒数法解决问题,灵活运用公式是解题个关键.

练习册系列答案
相关题目
13.在Rt△ABC中,∠C=90°,sinA=$\frac{1}{2}$,则∠A等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 不能确定 |
 如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是30cm2.求AD、CE的长.
如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是30cm2.求AD、CE的长.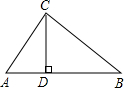 如图,在△ABC中,CD⊥AB于D,∠A=60°,∠B=45°,BC=4,
如图,在△ABC中,CD⊥AB于D,∠A=60°,∠B=45°,BC=4,