题目内容
已知，如图，圆O的弦AB=AD，∠BOD=124°，点C在劣弧 |
| BD |
| A、59° | B、62° |
| C、56° | D、42° |
考点：圆周角定理,圆心角、弧、弦的关系
专题：
分析：连接OA，先根据∠BOD=124°得出
的度数，再由圆O的弦AB=AD得出
=
，故可得出∠
AOD的度数，再由圆周角定理即可得出结论．
|
| DAB |
|
| AD |
|
| AB |
AOD的度数，再由圆周角定理即可得出结论．
解答：
解：∵∠BOD=124°
∴
=360°-124°=236°．
∵圆O的弦AB=AD，
∴
=
=
=118°，
∴∠AOD=118°，
∴∠DCA=
∠AOD=
×118°=59°．
故选A．
解：∵∠BOD=124°∴
|
| DAB |
∵圆O的弦AB=AD，
∴
|
| AD |
|
| AB |
| 236° |
| 2 |
∴∠AOD=118°，
∴∠DCA=
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
如图，已知点D为线段AC的中点，点B为线段DC的中点，DB=2，则线段AC=
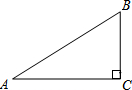在Rt△ABC中，∠C=90°，AB=10，tanA=| 3 |
| 4 |
| A、3 | B、4 | C、6 | D、8 |
为了进一步了解某校九年级学生的身体素质，体育老师从该年级各班中随机抽取50名学生进行1分钟跳绳次数测试，以测试数据为样本，绘制出如图表．盒中有3个白球，2个黄球，随机从中取出一个放回，再随即从盒中取出一个，则两次取出的都为黄球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，∠A=64°，∠ABD=22°，∠ACD=33°，求∠BDC的度数．已知x-y=0，下列等式不成立的是（ ）
| A、x=y | ||||
| B、3x=3y | ||||
| C、x=y+1 | ||||
D、
|